
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
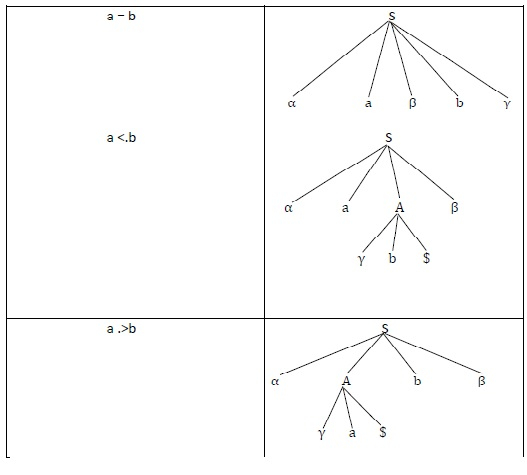
What are Precedence Relations in Operator Grammar?
For terminals a and b in an Operator Grammar we can have the following precedence Relations −
- a =. b(Equal Precedence) − If R.H.S of production is of form α a β b γ, where β can be ε or single non-terminal then a =. b.
Here, α and γ can be any strings.
Example − In grammar, S → m A c B e d
On Comparing mAcBed with αaβbγ
α = mA, a = c, β = B, b = e, γ = d
| Α | A | β | b | γ |
| mA | C | B | e | d |
So, comparing a with c and b with e we get c =.e.
We can also make a different combination for a and b.
In Grammar S → m A c Bed
α = ε, a = m, β = A, b = c, γ = Bed
| Α | A | β | b | γ |
| Ε | M | A | c | Bed |
So, comparing a with m and b with c
∴ m =. c
- a<.b (Less then)
If R.H.S of production is of form α a A β and A ?+ γb$ where γ is ε or single nonterminal then a <.b.
Example − In Grammar S → m A c D
A → i
On comparing m A c D with α a A β and A → i with A → γb$
| Α | A | A | β |
| Ε | M | A | cD |
| A → | Γ | b | $ |
| A → | E | i | ε |
∴ α = ε, a = m, A = A, β = cD
∴ γ = ε,
and b = i
∴ Applying the rule,
a <. b means m <. i
- a .> b (Greater Than)
If R.H.S of production is of form αAbβ and A ?+ γa$ where $ is ε or single nonterminal then a .> b.
Example − In Grammar S → m A c D
A → i
On comparing m A cD with α a bβ and A → i with A → γa$
| Α | A | b | β |
| M | A | c | D |
| Α → | Γ | a | $ |
| Α → | E | i | ε |
∴ α = m, A = A, b = c, β = D
On comparing i with γa $
∴ γ = ε, a = i, $ = ε
∴ On applying the rule,
a .> b means i .> c.
The Precedence relations between terminals symbols can also be shown by a Parse Tree −
Algorithm for Computing Operator Precedence Relations
Input − An Operator Grammar
Output − A Precedence Relations between terminals and symbols.
Method
- begin
- For each production A → B1, B2, … … … . Bn
for i = 1 to n – 1
If Bi and Bi+1 are both terminals then
set Bi = Bi+1
If i ≤ n − 2 and Bi and Bi+2are both terminals and Bi+1 is non-terminal then
set Bi = Bi+2
If Biis terminal & Bi+1is non-terminal then for all a in LEADING (Bi+1)
set Bi <. a
If Biis non-terminal & Bi+1 is terminal then for all a in TRAILING (Bi)
set a . > Bi+1
- end

