Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is unambiguous grammar in TOC?
A grammar can be unambiguous, if the grammar does not contain ambiguity. This means if it does not contain more than one left most derivation (LMD) or more than one right most derivation (RMD) or more than one parse tree for the given input string, it is an unambiguous grammar.
Rules
To convert the ambiguous grammar to the unambiguous grammar, we apply the following rules −
Rule 1 − If the left associative operators (+,-,*,/) are used in the production rule, then apply left recursion in the production rule. Left recursion is nothing but left most symbol on the right side is the same as the non-terminal on the left side.
X->Xa
Rule 2 − If the right associative operator (^) is used in the production rule then apply right recursion in the production rule.
Right recursion is nothing but right most symbols on the left side are the same as the nonterminal on the right side. For example, X->aX
Consider an example for the above mentioned rules.
Check whether the grammar is ambiguous or not.
A->AA
A->(A)
A->a
For the string "a(a)aa", the above grammar can generate two parse trees, as shown below
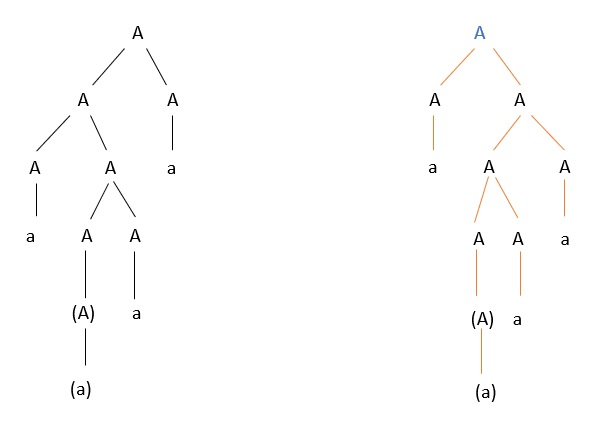
Since there are two parse trees, the grammar is ambiguous.
Consider another grammar
S->S+S
S->S*S
S->2
Let the parse tree is 2+2*2
The parse trees are given below −
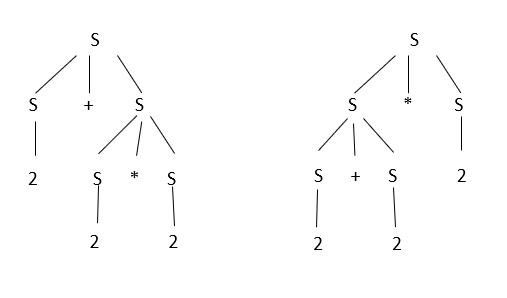
The given grammar is an ambiguous grammar. So, convert ambiguous grammar to unambiguous grammar by applying the associative rule, as explained below −
S->S+T
S->T
T->T*F
T->F
F->2
4K+ Views
