Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is a finite state machine in TOC?
A finite state machine has a set of states and two functions called the next-state and output function.
- The set of states correspond to all the possible combinations of the internal storage. If there are n bits of storage, there are 2n possible states.
- The next state function is a combinational logic function that, given the inputs and the current state, determines the next state of the system.
The diagram given below explains the functioning of a finite state machine in TOC.
The output function generates a set of outputs from the current state and the inputs.
Types
The two types of finite state machines are −
- Moore machine − In Moore machine, the output only depends on the current state.
- Mealy machine − In Mealy machine, the output depends on both the current state and the current input.
We mostly deal with the Moore machine. These two types are equivalent in capabilities.
A Finite State Machine consists of the following −
- K states: S = {s1, s2, ... ,sk}, s1 is initial state
- N inputs: I = {h, i2, ... ,in}
- M outputs: O = {o1, o2, . ,om}
- Next-state function T(S, I): This is used for mapping each current state and input to the next state.
- Output Function P(S): This function specifies the output.
Components
The components which exists in a finite state machine are explained below −
State − The states are usually drawn with circles and only one state can be active at a time.
It is represented as follows −
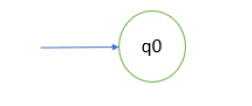
Initial State − It is the starting point of our system. Initial states are usually drawn with an arrow pointed to state, as shown below −
Final state − It is a subset of known states that indicates whether the input we processed is valid or not. Accepting states are usually drawn as a double circle as shown below −
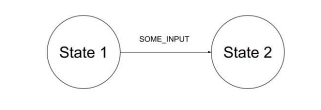
Transitions − The machine moves from one state to another and is indicated as transition. These are drawn as two states connected with a line, as shown below −
7K+ Views
To Continue Learning Please Login