Construct Finite State Machine as Processing input

Finite automata is an abstract computing device. It is a mathematical model of a system with discrete inputs, outputs, states and a set of transitions from state to state that occurs on input symbols from the alphabet Σ.

Formal definition of Finite Automata

Finite automata is defined as a 5-tuples

M=(Q, ∑, δ,q0,F)

Where,

• Q − Finite set called states.
• ∑ − Finite set called alphabets.
• δ − Q ☓ ∑ → Q is the transition function.
• q₀ ∈ Q is the start or initial state.
• F − Final or accept state.

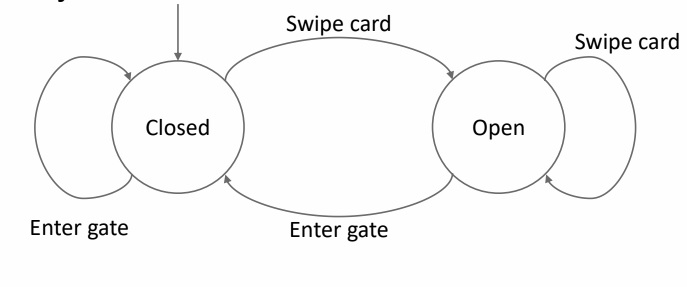
Consider the Oyster card barriers at tube stations −

States −

• Closed
• Open

Transitions −

• Swipe card
• Enter gate

Success − Will only withdraw credit, when a customer enters the gate.

FSM as processing input

Let us consider an example of the oyster card barriers at the tube stations. So, in order to show whether the transaction is accepted or rejected, let us consider the following input

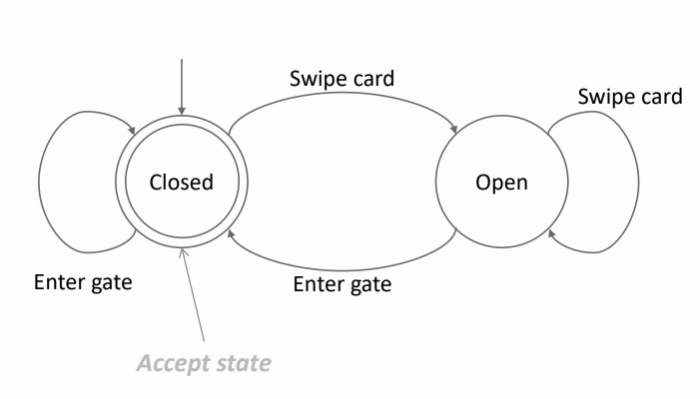
Accept state

The accept state for the oyster card barriers at the tube stations is given below −