Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
The Graph Coloring
Graph coloring is the procedure of assignment of colors to each vertex of a graph G such that no adjacent vertices get same color. The objective is to minimize the number of colors while coloring a graph. The smallest number of colors required to color a graph G is called its chromatic number of that graph. Graph coloring problem is a NP Complete problem.
Method to Color a Graph
The steps required to color a graph G with n number of vertices are as follows −
Step 1 − Arrange the vertices of the graph in some order.
Step 2 − Choose the first vertex and color it with the first color.
Step 3 − Choose the next vertex and color it with the lowest numbered color that has not been colored on any vertices adjacent to it. If all the adjacent vertices are colored with this color, assign a new color to it. Repeat this step until all the vertices are colored.
Example
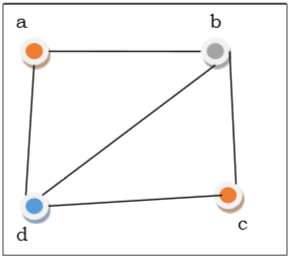
In the above figure, at first vertex a is colored red. As the adjacent vertices of vertex a are again adjacent, vertex b and vertex d are colored with different color, green and blue respectively. Then vertex c is colored as red as no adjacent vertex of c is colored red. Hence, we could color the graph by 3 colors. Hence, the chromatic number of the graph is 3.
Applications of Graph Coloring
Some applications of graph coloring include −
- Register Allocation
- Map Coloring
- Bipartite Graph Checking
- Mobile Radio Frequency Assignment
- Making time table, etc.
34K+ Views
