
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Coloring Graph
Graph coloring is nothing but a simple way of labelling graph components such as vertices, edges, and regions under some constraints. In a graph, no two adjacent vertices, adjacent edges, or adjacent regions are colored with minimum number of colors. This number is called the chromatic number and the graph is called a properly colored graph.
While graph coloring, the constraints that are set on the graph are colors, order of coloring, the way of assigning color, etc. A coloring is given to a vertex or a particular region. Thus, the vertices or regions having same colors form independent sets.
Vertex Coloring
Vertex coloring is an assignment of colors to the vertices of a graph ‘G’ such that no two adjacent vertices have the same color. Simply put, no two vertices of an edge should be of the same color.
Chromatic Number
The minimum number of colors required for vertex coloring of graph ‘G’ is called as the chromatic number of G, denoted by X(G).
χ(G) = 1 if and only if 'GX' is a null graph. If 'GX' is not a null graph, then χ(G) ≥ 2
Example
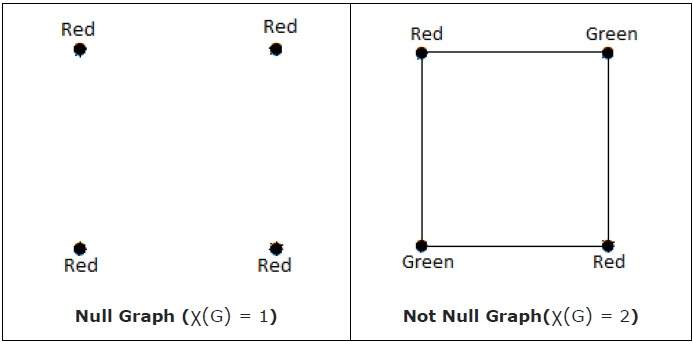
Note − A graph ‘G’ is said to be n-coverable if there is a vertex coloring that uses at most n colors, i.e., X(G) ≤ n.
Region Coloring
Region coloring is an assignment of colors to the regions of a planar graph such that no two adjacent regions have the same color. Two regions are said to be adjacent if they have a common edge.
Example
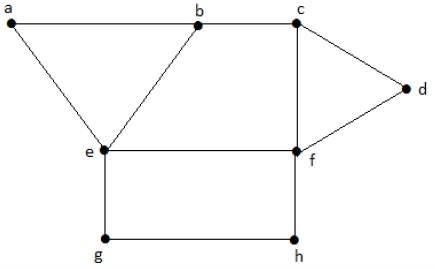
Take a look at the following graph. The regions ‘aeb’ and ‘befc’ are adjacent, as there is a common edge ‘be’ between those two regions.
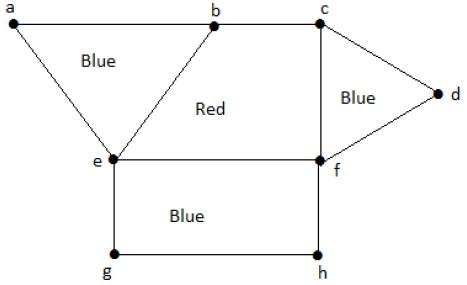
Similarly the other regions are also coloured based on the adjacency. This graph is coloured as follows −
Example
The chromatic number of Kn is
a) n
b) n–1
c) ⌊ n 2 ⌋
d) ⌈ n 2 ⌉
Consider this example with K4.
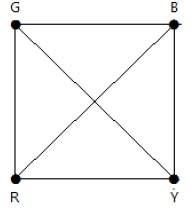
In the complete graph, each vertex is adjacent to remaining (n – 1) vertices. Hence, each vertex requires a new color. Hence the chromatic number of Kn = n.
Applications of Graph Coloring
Graph coloring is one of the most important concepts in graph theory. It is used in many real-time applications of computer science such as −
- Clustering
- Data mining
- Image capturing
- Image segmentation
- Networking
- Resource allocation
- Processes scheduling

