Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Edges and Vertices of Graph
A graph is a set of points, called nodes or vertices, which are interconnected by a set of lines called edges. The study of graphs, or graph theory is an important part of a number of disciplines in the fields of mathematics, engineering and computer science.
Graph Theory
Definition − A graph (denoted as G = (V, E)) consists of a non-empty set of vertices or nodes V and a set of edges E. A vertex a represents an endpoint of an edge. An edge joins two vertices a, b and is represented by set of vertices it connects.
Example − Let us consider, a Graph is G = (V, E) where V = {a, b, c, d} and E = {{a, b}, {a, c}, {b, c}, {c, d}}
Here V is verteces and a, b, c, d are various vertex of the graph.
Here E represents edges and {a, b}, {a, c}, {b, c}, {c, d} are various edge of the graph.
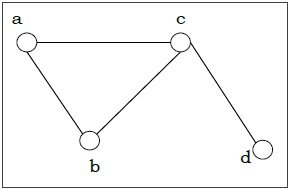
Degree of a Vertex − The degree of a vertex V of a graph G (denoted by deg (V)) is the number of edges incident with the vertex V.
| Vertex | Degree | Even / Odd |
|---|---|---|
| a | 2 | even |
| b | 2 | even |
| c | 3 | odd |
| d | 1 | odd |
Even and Odd Vertex − If the degree of a vertex is even, the vertex is called an even vertex and if the degree of a vertex is odd, the vertex is called an odd vertex.
Degree of a Graph − The degree of a graph is the largest vertex degree of that graph. For the above graph the degree of the graph is 3.
The Handshaking Lemma − In a graph, the sum of all the degrees of all the vertices is equal to twice the number of edges. For example, in above case, sum of all the degrees of all vertices is 8 and total edges are 4.
21K+ Views
