Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Graph Coloring
Graph coloring problem is a special case of graph labeling. In this problem, each node is colored into some colors. But coloring has some constraints. We cannot use the same color for any adjacent vertices.
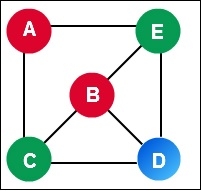
For solving this problem, we need to use the greedy algorithm, but it does not guaranty to use minimum color.
Input and Output
Input: Adjacency matrix of the graph. 0 0 1 0 1 0 0 1 1 1 1 1 0 1 0 0 1 1 0 1 1 1 0 1 0 Output: Node: 0, Assigned with Color: 0 Node: 1, Assigned with Color: 0 Node: 2, Assigned with Color: 1 Node: 3, Assigned with Color: 2 Node: 4, Assigned with Color: 1
Algorithm
graphColoring(graph)
Input − The given graph.
Output − Each node with some color assigned to it.
Begin declare a list of colors initially set the color 0 for first node define an array colorUsed to track which color is used, and which colors have never used. for all vertices i except first one, do mark i as unassigned to any color done mark colorUsed to false for all vertices for all vertices u in the graph except 1st vertex, do for all vertex v adjacent with u, do if color[v] is unassigned, then mark colorUsed[color[v]] := true done for all colors col in the color list, do if color is not used, then stop the loop done color[u] := col for each vertex v which is adjacent with u, do if color[v] is unassigned, then colorUsed[color[v]] := false done done for all vertices u in the graph, do display the node and its color done End
Example
#include<iostream>
#define NODE 6
using namespace std;
int graph[NODE][NODE] = {
{0, 1, 1, 1, 0, 0},
{1, 0, 0, 1, 1, 0},
{1, 0, 0, 1, 0, 1},
{1, 1, 1, 0, 1, 1},
{0, 1, 0, 1, 0, 1},
{0, 0, 1, 1, 1, 0}
};
void graphColoring() {
int color[NODE];
color[0] = 0; //Assign first color for the first node
bool colorUsed[NODE]; //Used to check whether color is used or not
for(int i = 1; i<NODE; i++)
color[i] = -1; //initialize all other vertices are unassigned
for(int i = 0; i<NODE; i++)
colorUsed[i] = false; //initially any colors are not chosen
for(int u = 1; u<NODE; u++) { //for all other NODE - 1 vertices
for(int v = 0; v<NODE; v++) {
if(graph[u][v]){
if(color[v] != -1) //when one color is assigned, make it unavailable
colorUsed[color[v]] = true;
}
}
int col;
for(col = 0; col<NODE; col++)
if(!colorUsed[col]) //find a color which is not assigned
break;
color[u] = col; //assign found color in the list
for(int v = 0; v<NODE; v++) { //for next iteration make color availability to false
if(graph[u][v]) {
if(color[v] != -1)
colorUsed[color[v]] = false;
}
}
}
for(int u = 0; u<NODE; u++)
cout <<"Color: " << u << ", Assigned with Color: " <<color[u] <<endl;
}
main() {
graphColoring();
}Output
Node: 0, Assigned with Color: 0 Node: 1, Assigned with Color: 0 Node: 2, Assigned with Color: 1 Node: 3, Assigned with Color: 2 Node: 4, Assigned with Color: 1
Updated on: 16-Jun-2020
5K+ Views
Advertisements