Reading a point in the coordinate plane

In the quadrant 1, both the x coordinate and the y coordinate are positive.

The signs of the ordered pairs in quadrant 1 are (+, +)

In the quadrant 2, the x coordinate is negative and the y coordinate is positive.

The signs of the ordered pairs in quadrant 2 are (−, +)

In the quadrant 3, both the x coordinate and the y coordinate are negative.

The signs of the ordered pairs in quadrant 3 are (−, −)

In the quadrant 4, the x coordinate is positive and the y coordinate is negative.

The signs of the ordered pairs in quadrant 4 are (+, −)

Rules for reading a point in coordinate plane

• The quadrant in which the given point is located is found by looking at the signs of its x and y coordinates.

• We then read the number of units the point is to the right/left of the origin along the x axis to find its x coordinate.

• We also read the number of units the point is above/below the origin along the y axis to find its y coordinate.

• The x and y coordinates of the given point give its location in terms of an ordered pair. This is how a point in the coordinate plane is read.

Give the location of Atlanta as an ordered pair (x, y) from the grid given below.

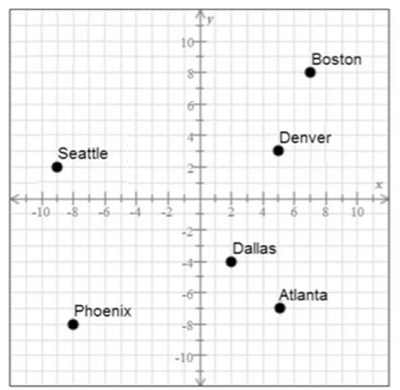
Solution

Step 1 − To get the first or x coordinate we move to the right 5 units from the origin (0, 0). Since it is to right, it is positive so the x co-ordinate is +5. To get the second or y coordinate we move down 7 units from the origin (0, 0). Since it is moving down it is negative and the y coordinate is −7.

Since x is positive and y is negative, Atlanta lies in fourth quadrant.

Step 2 − So we read the coordinates of Atlanta as (5, −7).

Give the coordinates of the shapes lightning, diamond and letter K as ordered pair (x, y)

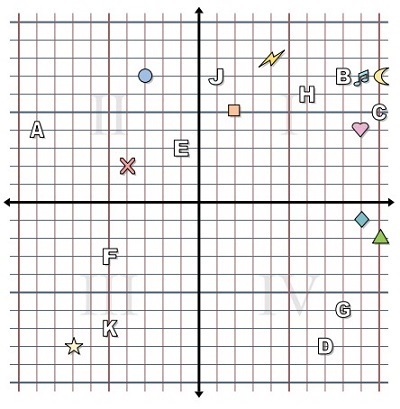
Solution

Step 1 − The coordinates for the lightning shape are got by moving four units to the right of origin along x axis and then moving vertically up eight units. They are (4, 8). This shape lies in quadrant 1.

Step 2 − The coordinates for the diamond shape are got by moving nine units to the right of origin along x axis and then moving vertically down one unit. They are (9, −1). This shape lies in quadrant 4.

Step 3 − The coordinates for the letter ‘K’ are got by moving five units to the left of origin along x axis and then moving vertically down seven units. They are (−5, −7). This letter lies in quadrant 3.