Plotting a point in quadrant 1: Mixed number coordinates

Introduction

The coordinate plane has a vertical line and a horizontal line intersecting in the origin. Usually whole numbers are represented on the x axis and the y axis. However, in this lesson we are going to learn how to plot points that have mixed number coordinates in the quadrant 1.

Example

Consider the example −

Plot the following point in the quadrant 1

(1, 2 )

Solution

We see that the x coordinate is 1. And y coordinate is 2. Each of the unit division along x axis represented by whole numbers is divided into 3 equal parts, , or 2 and so on. While those along the y axis are divided into 4 equal parts..., and so on.

Example 1

Plot the following point in the quadrant 1.

(5, 2 )

Solution

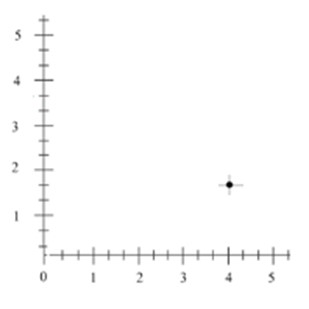
Step 1 − The x coordinate and y coordinate of the point are 5 and 2respectively and the point lies in the quadrant 1.

Step 2 − Each of the unit divisions along x axis and the y axis represented by whole numbers is divided into 3 equal parts.

Step 3 − Plotting the point (5, 2 ) in the quadrant 1 we get

Example 2

Plot the following point in the quadrant 1

(4, 1)

Solution

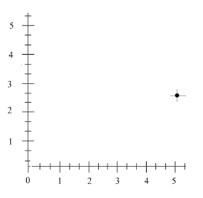
Step 1 − The x coordinate and y coordinate of the point are 4 and 1respectively and the point lies on the positive y axis.

Step 2 − Each of the unit divisions along x axis and the y axis represented by whole numbers is divided into 3 equal parts.

Step 3 − Plotting the point (4, 1) in the quadrant 1 we get.