
- Ordered Pairs
- Home
- Reading a point in quadrant 1
- Plotting a point in quadrant 1
- Reading a point in the coordinate plane
- Plotting a point in the coordinate plane
- Plotting a point in quadrant 1: Mixed number coordinates
- Plotting a point in the coordinate plane: Mixed number coordinates
- Naming the quadrant or axis of a point given its graph
- Naming the quadrant or axis of a point given its coordinates
- Naming the quadrant or axis of a point the signs of its coordinates
- Finding distances between points that share a common coordinate given the graph
- Finding distances between points that share a common coordinate given their coordinates
Finding distances between points that share a common coordinate given the graph Online Quiz
Following quiz provides Multiple Choice Questions (MCQs) related to Finding distances between points that share a common coordinate given the graph. You will have to read all the given answers and click over the correct answer. If you are not sure about the answer then you can check the answer using Show Answer button. You can use Next Quiz button to check new set of questions in the quiz.

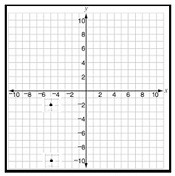
Answer : A
Explanation
Step 1 − The coordinates of the pair of points are (5, 2) and (5, 10).
Step 2 − The distance between the pair of points is the difference between their y coordinates as x coordinates are same.
Step 3 − The distance between the pair of points = 2 (10) = 2 + 10 = 8 units.
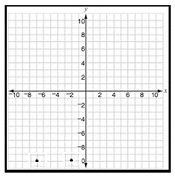
Answer : C
Explanation
Step 1 − The coordinates of the pair of points are (2, 10) and (7, 10).
Step 2 − The distance between the pair of points is the difference between their x coordinates as y coordinates are same.
Step 3 − The distance between the pair of points = 2 (7) = 2 + 7 = 5 units.
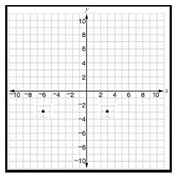
Answer : B
Explanation
Step 1 − The coordinates of the pair of points are (3, 3) and (6, 3).
Step 2 − The distance between the pair of points is the difference between their x coordinates as y coordinates are same.
Step 3 − The distance between the pair of points = 3 (6) = 3 + 6 = 9 units.
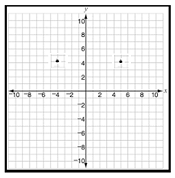
Answer : D
Explanation
Step 1 − The coordinates of the pair of points are (5, 4) and (4, 4).
Step 2 − The distance between the pair of points is the difference between their x coordinates as y coordinates are same.
Step 3 − The distance between the pair of points = 5 (4) = 5 + 4 = 9 units.
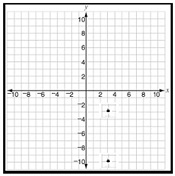
Answer : B
Explanation
Step 1 − The coordinates of the pair of points are (3, 3) and (3, 10).
Step 2 − The distance between the pair of points is the difference between their y coordinates as x coordinates are same.
Step 3 − The distance between the pair of points = 3 (10) = 3 + 10 = 7 units.

Answer : A
Explanation
Step 1 − The coordinates of the pair of points are (9, 2) and (9, 5).
Step 2 − The distance between the pair of points is the difference between their y coordinates as x coordinates are same.
Step 3 − The distance between the pair of points = 2 (5) = 2 + 5 = 7 units
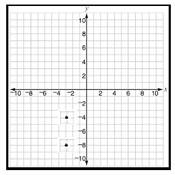
Answer : C
Explanation
Step 1 − The coordinates of the pair of points are (3, 4) and (3, 8).
Step 2 − The distance between the pair of points is the difference between their y coordinates as x coordinates are same.
Step 3 − The distance between the pair of points = 4 (8) = 4 + 8 = 4 units.
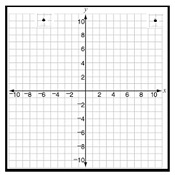
Answer : D
Explanation
Step 1 − The coordinates of the pair of points are (6, 10) and (10, 10).
Step 2 − The distance between the pair of points is the difference between their x coordinates as y coordinates are same.
Step 3 − The distance between the pair of points = 10 (6) = 10 + 6 = 16 units

Answer : C
Explanation
Step 1 − The coordinates of the pair of points are (3, 10) and (3, 4).
Step 2 − The distance between the pair of points is the difference between their y coordinates as x coordinates are same.
Step 3 − The distance between the pair of points = 10 4 = 6 units.
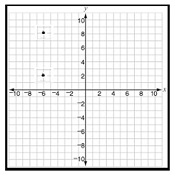
Answer : A
Explanation
Step 1 − The coordinates of the pair of points are (6, 2) and (6, 8).
Step 2 − The distance between the pair of points is the difference between their y coordinates as x coordinates are same.
step 3 − The distance between the pair of points = 8 2 = 6 units