Trapezoidal Rule for definite integral

Definite integrals can be solved using this trapezoidal rule. To integrate a function f(x) between the range a to b is basically finding the area below the curve from point x = a to x = b. 

To find that area, we can divide the area into n trapezoids, and the width of each trapezoid is h, so we can say that (b - a) = nh. When the number of trapezoids increases, the result of area calculation will be more accurate. To solve integrals, we will follow this formula.

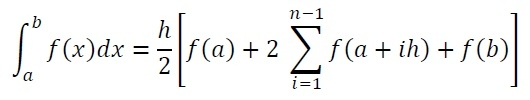
Here h is the width of the interval, and n is the number of intervals. We can find the h by using 

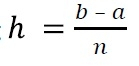
Input and Output

Input:
The function f(x): 1-exp(-x/2.0) and limits of the integration: 0, 1. The number of intervals: 20
Output:
The answer is: 0.21302

Algorithm

integrateTrapezoidal(a, b, n)

Input: Lower and upper limit, and the number of integrals n.

Output: The result of integration.

Begin
   h := (b - a)/n
   sum := f(a) + f(b)
   for i := 1 to n, do
      sum := sum + f(a + ih)
   done
   return sum
End

Example

#include<iostream>
#include<cmath>
using namespace std;

float mathFunc(float x) {
   return (1-exp(-x/2.0));    //the function 1 - e^(-x/2)
}

float integrate(float a, float b, int n) {
   float h, sum;
   int i;
   h = (b-a)/n;    //calculate the distance between two interval
   sum = (mathFunc(a)+mathFunc(b))/2;    //initial sum using f(a) and f(b)

   for(i = 1; i<n; i++) {
      sum += mathFunc(a+i*h);
   }
   return (h*sum);    //The result of integration
}

main() {
   float result, lowLim, upLim;
   int interval;
   cout << "Enter Lower Limit, Upper Limit and interval: "; cin >>lowLim >>upLim >>interval;
   result = integrate(lowLim, upLim, interval);
   cout << "The answer is: " << result;
}

Output

Enter Lower Limit, Upper Limit and interval: 0 1 20
The answer is: 0.21302