Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Euler and Hamiltonian Paths
A graph is traversable if you can draw a path between all the vertices without retracing the same path. Based on this path, there are some categories like Euler’s path and Euler’s circuit which are described in this chapter.
Euler’s Path
An Euler’s path contains each edge of ‘G’ exactly once and each vertex of ‘G’ at least once. A connected graph G is said to be traversable if it contains an Euler’s path.
Example
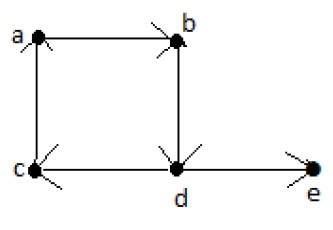
Euler’s Path = d-c-a-b-d-e.
Euler’s Circuit
In an Euler’s path, if the starting vertex is same as its ending vertex, then it is called an Euler’s circuit.
Example
Euler’s Path = a-b-c-d-a-g-f-e-c-a.
Euler’s Circuit Theorem
A connected graph ‘G’ is traversable if and only if the number of vertices with odd degree in G is exactly 2 or 0. A connected graph G can contain an Euler’s path, but not an Euler’s circuit, if it has exactly two vertices with an odd degree.
Note − This Euler path begins with a vertex of odd degree and ends with the other vertex of odd degree.
Example
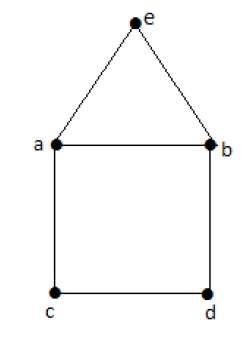
Euler’s Path − b-e-a-b-d-c-a is not an Euler’s circuit, but it is an Euler’s path. Clearly it has exactly 2 odd degree vertices.
Note − In a connected graph G, if the number of vertices with odd degree = 0, then Euler’s circuit exists.
Hamiltonian Path
A connected graph is said to be Hamiltonian if it contains each vertex of G exactly once. Such a path is called a Hamiltonian path.
Example
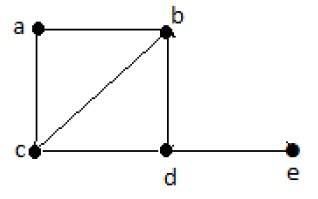
Hamiltonian Path − e-d-b-a-c.
Note −
- Euler’s circuit contains each edge of the graph exactly once.
- In a Hamiltonian cycle, some edges of the graph can be skipped.
Example
Take a look at the following graph −
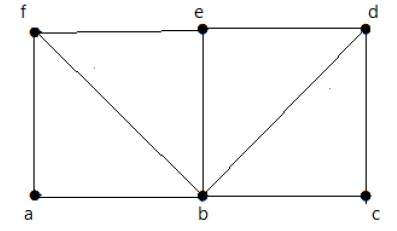
For the graph shown above −
- Euler path exists – false
- Euler circuit exists – false
- Hamiltonian cycle exists – true
- Hamiltonian path exists – true
G has four vertices with odd degree, hence it is not traversable. By skipping the internal edges, the graph has a Hamiltonian cycle passing through all the vertices.
6K+ Views
