Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Prove that the Hamiltonian Path is NP-Complete in TOC
A Hamilton cycle is a round trip path along n edges of graph G which visits every vertex once and returns to its starting vertex
Example
Given below is an example of the Hamilton cycle path −
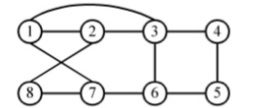
Hamilton cycle path: 1,2,8,7,6,5,4,3,1
TSP is NP-Complete
The travelling salesman problem (TSP) is having a salesman and a set of cities. The salesman needs to visit each one of the cities starting from a certain one and returning to the same city i.e. back to starting position. The challenge of this problem is that the travelling salesman wants to minimise the total length of the trip.
Proof
To prove TSP is NP-Complete, first try to prove TSP belongs to Non-deterministic Polynomial (NP).
In TSP, we have to find a tour and check that the tour contains each vertex once.
Then, we calculate the total cost of the edges of the tour. Finally, we check if the cost is minimum or not. This can be done in polynomial time.
Therefore, TSP belongs to NP.
Next, we have to prove that TSP is NP-hard.
To prove this, one way is to show that the Hamiltonian cycle ≤p TSP (as we know that the Hamiltonian cycle problem is NP Complete).
Assume G = (V, E) to be an instance of the Hamiltonian cycle.
Hence, an instance of TSP is constructed. We can create the complete graph G' = (V, E'), where
E′={(i,j):i,j∈Vandi≠j
Thus, the cost function is defined as follows:
t(i,j)= 0 if (i,j) ∈ E
=1 otherwiseNow, assume that a Hamiltonian cycle H exists in G. The cost of each edge in H is 0 in G' as each edge belongs to E. Therefore, H is having a cost of 0 in G'. Thus, if graph G has a Hamiltonian cycle, then graph G' has a tour of 0 cost.
Now let us assume that G' has a tour H’ of cost at most 0. The cost of edges in E' are 0 and 1 by definition. Hence, each edge must have a cost of 0 as the cost of H’ is 0. We finally conclude that H' contains only edges in E.
Finally proved that G has a Hamiltonian cycle, if and only if G' has a tour of cost at most 0. TSP is NP-complete.
4K+ Views
