Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Strongly Connected Graphs
In a directed graph is said to be strongly connected, when there is a path between each pair of vertices in one component.
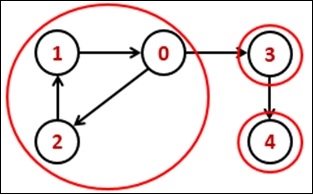
To solve this algorithm, firstly, DFS algorithm is used to get the finish time of each vertex, now find the finish time of the transposed graph, then the vertices are sorted in descending order by topological sort.
Input and Output
Input: Adjacency matrix of the graph. 0 0 1 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 Output: Following are strongly connected components in given graph: 0 1 2 3 4
Algorithm
traverse(graph, start, visited)
Input: The graph which will be traversed, the starting vertex, and flags of visited nodes.
Output: Go through each node in the DFS technique and display nodes.
Begin mark start as visited for all vertices v connected with start, do if v is not visited, then traverse(graph, v, visited) done End
topoSort(u, visited, stack)
Input − The start node, flag for visited vertices, stack.
Output − Fill stack while sorting the graph.
Begin mark u as visited for all node v, connected with u, do if v is not visited, then topoSort(v, visited, stack) done push u into the stack End
getStrongConComponents(graph)
Input: The given graph.
Output − All strongly connected components.
Begin initially all nodes are unvisited for all vertex i in the graph, do if i is not visited, then topoSort(i, vis, stack) done make all nodes unvisited again transGraph := transpose of given graph while stack is not empty, do pop node from stack and take into v if v is not visited, then traverse(transGraph, v, visited) done End
Example
#include <iostream>
#include <stack>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {
{0, 0, 1, 1, 0},
{1, 0, 0, 0, 0},
{0, 1, 0, 0, 0},
{0, 0, 0, 0, 1},
{0, 0, 0, 0, 0}
};
int transGraph[NODE][NODE];
void transpose() { //transpose the graph and store to transGraph
for(int i = 0; i<NODE; i++)
for(int j = 0; j<NODE; j++)
transGraph[i][j] = graph[j][i];
}
void traverse(int g[NODE][NODE], int u, bool visited[]) {
visited[u] = true; //mark v as visited
cout << u << " ";
for(int v = 0; v<NODE; v++) {
if(g[u][v]) {
if(!visited[v])
traverse(g, v, visited);
}
}
}
void topoSort(int u, bool visited[], stack<int>&stk) {
visited[u] = true; //set as the node v is visited
for(int v = 0; v<NODE; v++) {
if(graph[u][v]) { //for allvertices v adjacent to u
if(!visited[v])
topoSort(v, visited, stk);
}
}
stk.push(u); //push starting vertex into the stack
}
void getStrongConComponents() {
stack<int> stk;
bool vis[NODE];
for(int i = 0; i<NODE; i++)
vis[i] = false; //initially all nodes are unvisited
for(int i = 0; i<NODE; i++)
if(!vis[i]) //when node is not visited
topoSort(i, vis, stk);
for(int i = 0; i<NODE; i++)
vis[i] = false; //make all nodes are unvisited for traversal
transpose(); //make reversed graph
while(!stk.empty()) { //when stack contains element, process in topological order
int v = stk.top(); stk.pop();
if(!vis[v]) {
traverse(transGraph, v, vis);
cout << endl;
}
}
}
int main() {
cout << "Following are strongly connected components in given graph: "<<endl;
getStrongConComponents();
}Output
Following are strongly connected components in given graph: 0 1 2 3 4
3K+ Views
