Adaptive Merging and Sorting in Data Structure

ADAPTIVE MERGE SORT

Adaptive Merge Sort performs the merging of sorted sub-list merge sort does. However, the size of initial sub-list is depended upon the existence of ordering among the list of elements rather than having sub-list of size 1. For example, consider list in the figure.

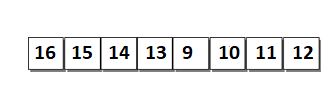
It consists of 2 sorted sub-lists.

• sub-list 1 with elements 16,15,14,13.
• sub-list 2 with elements 9,10,11,12.

The sub-list 1 is sorted but in reverse order. Thus, the sub-list 1 is reversed as shown in the figure.

Once the sub-lists are found merging process starts. Adaptive merge sort starts merging the sub-lists. Adaptive merge sort will need only one merging step as there are only 2 sub- lists. The result of merging is shown in figure.

Design Idea

• Begin by finding the sub-lists which are already sorted in required or reverse order
• If there exist any sub-list with elements in reverse order, then reverse the sub-list by exchanging 1st element with last, 2nd element with 2nd last and it is continued.
• Keep on merging sub-lists to produce new sub-lists until and unless is only 1 sub-list remaining.

Adaptive Merge Sort Analysis

Adaptive merge sort instead of beginning with sub-list of size 1, finds a sub-list which are already in sorted in required or reverse order. The size of sub-lists found initially would be minimum 2 and maximum m (m is the number of elements).

However, if the sub-list contains elements in reverse order, then it reverses the list before starting a merge operation. The reversal of list requires (m/2) exchange operations.

Best Case

If list is already in sorted order or in reverse order, then the Adaptive merge sort will have only one list and will not require any merge operation. However, finding that the list is already sorted will require O(m) comparison operation and (m/2) exchange operation if the list is sorted in reverse order. This makes the Adaptive Merge sort adaptive even when the list sorted in reverse order.

Thus the Time complexity for best case is calculated as follows −

T(m) = (m-1)+(m/2)
T(m) = (2m-2+m)/2
T(m) = O(m).

However, Adaptive merge sort implements additional space of O(m) in comparison of merge sort

Worst Case

Adaptive merge sort will find sub-list which is already sorted in required or reverse order. However, in worst case there are no partial or total ordering elements. Thus, the sub-list found initially would be of size 2. Once the sub-lists are found the merging process starts.

• merging sub-lists of size 2 results in sorted sub-list of size 4.
• merging sub-lists of size 4 results in sorted sub-list of size 8.
• The process of merging goes on until and unless 2k < m. where k is the kth merging step.

Since the merging steps in worst case of Adaptive merge sort is same as merge sort. Thus, the Time Complexity for worst case of Adaptive merge sort is similar as merge sort −

T(m) = O(m log m).