
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Compressed Quadtrees and Octrees in Data Structure
Compressed Quadtrees
At the time of storing every node corresponding to a subdivided cell, we may end up storing a lot of empty nodes. Cutting down on the size of such sparse trees is possible by only storing subtrees whose leaves have interesting data (i.e. "important subtrees"). Again we can actually cut down on the size even further. When we only consider important subtrees, the pruning process may avoid long paths in the tree where the intermediate nodes have degree two (a link to one parent and one child). It turns out that we only require to store the node U at the starting of this path (and associate some meta-data with it to represent the deleted nodes) and attach the subtree rooted at its end to U. These compressed trees still have a linear height when given "bad" input points.
Although we cut down a lot of the tree when we perform this compression, it is still possible to achieve logarithmic-time insertion, deletion and search by taking advantage of Z-order curves. The Z-order curve converts each cell of the full quadtree (and hence even the compressed quadtree) in O(1) time to a 1-dimensional line (and converts it back in O(1) time too), building a total order on the elements. Now, we can be able to store the quadtree in a data structure for ordered sets(in which we store the nodes of the tree). Now, we must state a reasonable assumption prior to continue: we assume that given two real numbers α,β € [0,1] denoted as binary, we can calculate in O(1) time the index of the first bit in which they differ. We also assume that we can calculate in O(1) time the smallest common ancestor of two points/cells in the quadtree and establish their relative Z-ordering, and we can calculate the floor function in O(1) time. With these assumptions, point location of a given point Q (i.e. find the cell that would contain Q), deletion and insertion operations can all be performed in O(n log n) time (i.e. the time it takes to perform a search in the underlying ordered set data structure).
To perform a point location for Q (i.e. determining its cell in the compressed tree)
- The existing cell is found in the compressed tree that comes before Q in the Z-order. Call this cell V.
- If Q€V is performed, return V.
- Else, find what would have been the smallest common ancestor of the point Q and the cell V in an uncompressed quadtree. Call this ancestor cell U.
- Find the existing cell in the compressed tree that comes prior to U in the Z-order and return it.
Without going into specific details, to perform insertions and deletions we first perform a point location for the thing we want to insert/delete, and then insert/delete it. Care must be taken to reshape the tree as appropriate, building and deleting nodes as required.
Octree
An octree is defined as a tree data structure in which each internal node is associated with exactly eight children.
Octrees are most often implemented to partition a 3-dimensional space by recursively subdividing it into eight octants.
Octrees are treated as the 3-dimensional analog of quadtrees. The name is created from oct + tree, but note that it is normally written "octree" with only one "t".
Octrees are often implemented in 3D graphics and 3D game engines.
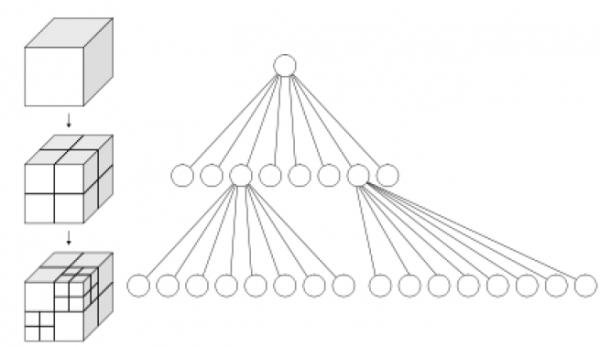
For spatial representation
Each node in an octree is responsible to subdivide the space it represents into eight octants. In a point region (PR)
octree, the node stores an explicit 3-dimensional point, which is the "center" of the subdivision for that node; the point
specifies one of the corners for each of the eight children. In case of a matrix based (MX) octree, the subdivision point is implicitly the center of the space represented by the node. The root node of a PR octree can be able to represent infinite space; the root node of an MX octree must be able to represent a finite bounded space so that the implicit centers are well-defined.
Common uses
- Level of detail rendering in 3D computer graphics
- Spatial indexing
- Searching nearest neighbour
- Efficient collision detection in three dimensions
- Analysis of finite element
- Sparse voxel octree
- Estimation of state
- Estimation of set

