Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Eulerian Path and Circuit
The Euler path is a path, by which we can visit every edge exactly once. We can use the same vertices for multiple times. The Euler Circuit is a special type of Euler path. When the starting vertex of the Euler path is also connected with the ending vertex of that path, then it is called the Euler Circuit.
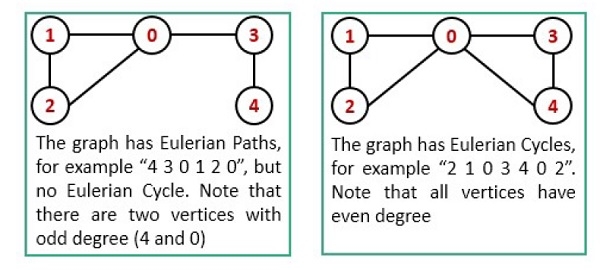
To detect the path and circuit, we have to follow these conditions −
- The graph must be connected.
- When exactly two vertices have odd degree, it is a Euler Path.
- Now when no vertices of an undirected graph have odd degree, then it is a Euler Circuit.
Input and Output
Input: Adjacency matrix of a graph. 0 1 1 1 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 1 0 0 0 1 0 Output: The graph has an Eulerian path.
Algorithm
traverse(u, visited)
Input: The start node u and the visited node to mark which node is visited.
Output − Traverse all connected vertices.
Begin mark u as visited for all vertex v, if it is adjacent with u, do if v is not visited, then traverse(v, visited) done End
isConnected(graph)
Input − The graph.
Output − True if the graph is connected.
Begin define visited array for all vertices u in the graph, do make all nodes unvisited traverse(u, visited) if any unvisited node is still remaining, then return false done return true End
isEulerian(Graph)
Input − The given Graph.
Output − Returns 0, when not Eulerian, 1 when it has a Euler path, 2 when Euler circuit found
Begin if isConnected() is false, then return false define list of degree for each node oddDegree := 0 for all vertex i in the graph, do for all vertex j which are connected with i, do increase degree done if degree of vertex i is odd, then increase dooDegree done if oddDegree > 2, then return 0 if oddDegree = 0, then return 2 else return 1 End
Example
#include<iostream>
#include<vector>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {
{0, 1, 1, 1, 0},
{1, 0, 1, 0, 0},
{1, 1, 0, 0, 0},
{1, 0, 0, 0, 1},
{0, 0, 0, 1, 0}
};
/* int graph[NODE][NODE] = {
{0, 1, 1, 1, 1},
{1, 0, 1, 0, 0},
{1, 1, 0, 0, 0},
{1, 0, 0, 0, 1},
{1, 0, 0, 1, 0}
};
*/ //uncomment to check Euler Circuit
/* int graph[NODE][NODE] = {
{0, 1, 1, 1, 0},
{1, 0, 1, 1, 0},
{1, 1, 0, 0, 0},
{1, 1, 0, 0, 1},
{0, 0, 0, 1, 0}
};
*/ //Uncomment to check Non Eulerian Graph
void traverse(int u, bool visited[]) {
visited[u] = true; //mark v as visited
for(int v = 0; v<NODE; v++) {
if(graph[u][v]) {
if(!visited[v])
traverse(v, visited);
}
}
}
bool isConnected() {
bool *vis = new bool[NODE];
//for all vertex u as start point, check whether all nodes are visible or not
for(int u; u < NODE; u++) {
for(int i = 0; i<NODE; i++)
vis[i] = false; //initialize as no node is visited
traverse(u, vis);
for(int i = 0; i<NODE; i++) {
if(!vis[i]) //if there is a node, not visited by traversal, graph is not connected
return false;
}
}
return true;
}
int isEulerian() {
if(isConnected() == false) //when graph is not connected
return 0;
vector<int> degree(NODE, 0);
int oddDegree = 0;
for(int i = 0; i<NODE; i++) {
for(int j = 0; j<NODE; j++) {
if(graph[i][j])
degree[i]++; //increase degree, when connected edge found
}
if(degree[i] % 2 != 0) //when degree of vertices are odd
oddDegree++; //count odd degree vertices
}
if(oddDegree > 2) //when vertices with odd degree greater than 2
return 0;
return (oddDegree)?1:2; //when oddDegree is 0, it is Euler circuit, and when 2, it is Euler path
}
int main() {
int check;
check = isEulerian();
switch(check) {
case 0: cout << "The graph is not an Eulerian graph.";
break;
case 1: cout << "The graph has an Eulerian path.";
break;
case 2: cout << "The graph has a Eulerian circuit.";
break;
}
}Output
The graph has an Eulerian path.
Updated on: 16-Jun-2020
6K+ Views
Advertisements