
- Digital Communication - Home
- Analog to Digital
- Pulse Code Modulation
- Sampling
- Quantization
- Differential PCM
- Delta Modulation
- Techniques
- Line Codes
- Data Encoding Techniques
- Pulse Shaping
- Digital Modulation Techniques
- Amplitude Shift Keying
- Frequency Shift Keying
- Phase Shift Keying
- Quadrature Phase Shift Keying
- Differential Phase Shift Keying
- M-ary Encoding
- Information Theory
- Source Coding Theorem
- Channel Coding Theorem
- Error Control Coding
- Spread Spectrum Modulation
Digital Communication - Quick Guide
Digital Communication - Analog to Digital
The communication that occurs in our day-to-day life is in the form of signals. These signals, such as sound signals, generally, are analog in nature. When the communication needs to be established over a distance, then the analog signals are sent through wire, using different techniques for effective transmission.
The Necessity of Digitization
The conventional methods of communication used analog signals for long distance communications, which suffer from many losses such as distortion, interference, and other losses including security breach.
In order to overcome these problems, the signals are digitized using different techniques. The digitized signals allow the communication to be more clear and accurate without losses.
The following figure indicates the difference between analog and digital signals. The digital signals consist of 1s and 0s which indicate High and Low values respectively.

Advantages of Digital Communication
As the signals are digitized, there are many advantages of digital communication over analog communication, such as −
The effect of distortion, noise, and interference is much less in digital signals as they are less affected.
Digital circuits are more reliable.
Digital circuits are easy to design and cheaper than analog circuits.
The hardware implementation in digital circuits, is more flexible than analog.
The occurrence of cross-talk is very rare in digital communication.
The signal is un-altered as the pulse needs a high disturbance to alter its properties, which is very difficult.
Signal processing functions such as encryption and compression are employed in digital circuits to maintain the secrecy of the information.
The probability of error occurrence is reduced by employing error detecting and error correcting codes.
Spread spectrum technique is used to avoid signal jamming.
Combining digital signals using Time Division Multiplexing (TDM) is easier than combining analog signals using Frequency Division Multiplexing (FDM).
The configuring process of digital signals is easier than analog signals.
Digital signals can be saved and retrieved more conveniently than analog signals.
Many of the digital circuits have almost common encoding techniques and hence similar devices can be used for a number of purposes.
The capacity of the channel is effectively utilized by digital signals.
Elements of Digital Communication
The elements which form a digital communication system is represented by the following block diagram for the ease of understanding.
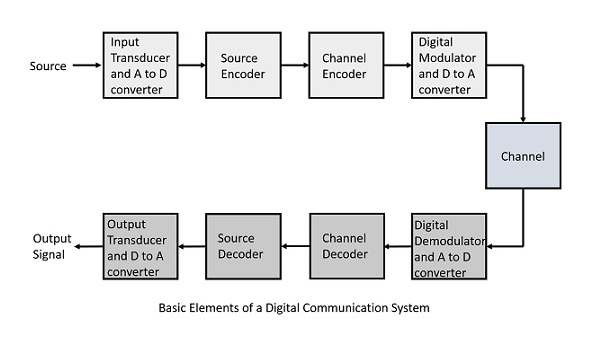
Following are the sections of the digital communication system.
Source
The source can be an analog signal. Example: A Sound signal
Input Transducer
This is a transducer which takes a physical input and converts it to an electrical signal (Example: microphone). This block also consists of an analog to digital converter where a digital signal is needed for further processes.
A digital signal is generally represented by a binary sequence.
Source Encoder
The source encoder compresses the data into minimum number of bits. This process helps in effective utilization of the bandwidth. It removes the redundant bits (unnecessary excess bits, i.e., zeroes).
Channel Encoder
The channel encoder, does the coding for error correction. During the transmission of the signal, due to the noise in the channel, the signal may get altered and hence to avoid this, the channel encoder adds some redundant bits to the transmitted data. These are the error correcting bits.
Digital Modulator
The signal to be transmitted is modulated here by a carrier. The signal is also converted to analog from the digital sequence, in order to make it travel through the channel or medium.
Channel
The channel or a medium, allows the analog signal to transmit from the transmitter end to the receiver end.
Digital Demodulator
This is the first step at the receiver end. The received signal is demodulated as well as converted again from analog to digital. The signal gets reconstructed here.
Channel Decoder
The channel decoder, after detecting the sequence, does some error corrections. The distortions which might occur during the transmission, are corrected by adding some redundant bits. This addition of bits helps in the complete recovery of the original signal.
Source Decoder
The resultant signal is once again digitized by sampling and quantizing so that the pure digital output is obtained without the loss of information. The source decoder recreates the source output.
Output Transducer
This is the last block which converts the signal into the original physical form, which was at the input of the transmitter. It converts the electrical signal into physical output (Example: loud speaker).
Output Signal
This is the output which is produced after the whole process. Example − The sound signal received.
This unit has dealt with the introduction, the digitization of signals, the advantages and the elements of digital communications. In the coming chapters, we will learn about the concepts of Digital communications, in detail.
Pulse Code Modulation
Modulation is the process of varying one or more parameters of a carrier signal in accordance with the instantaneous values of the message signal.
The message signal is the signal which is being transmitted for communication and the carrier signal is a high frequency signal which has no data, but is used for long distance transmission.
There are many modulation techniques, which are classified according to the type of modulation employed. Of them all, the digital modulation technique used is Pulse Code Modulation (PCM).
A signal is pulse code modulated to convert its analog information into a binary sequence, i.e., 1s and 0s. The output of a PCM will resemble a binary sequence. The following figure shows an example of PCM output with respect to instantaneous values of a given sine wave.
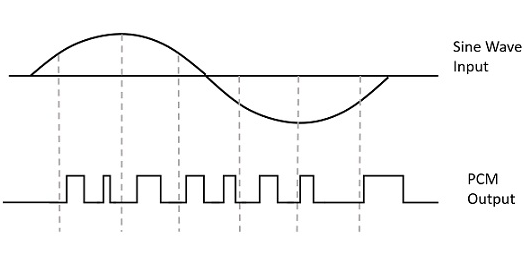
Instead of a pulse train, PCM produces a series of numbers or digits, and hence this process is called as digital. Each one of these digits, though in binary code, represent the approximate amplitude of the signal sample at that instant.
In Pulse Code Modulation, the message signal is represented by a sequence of coded pulses. This message signal is achieved by representing the signal in discrete form in both time and amplitude.
Basic Elements of PCM
The transmitter section of a Pulse Code Modulator circuit consists of Sampling, Quantizing and Encoding, which are performed in the analog-to-digital converter section. The low pass filter prior to sampling prevents aliasing of the message signal.
The basic operations in the receiver section are regeneration of impaired signals, decoding, and reconstruction of the quantized pulse train. Following is the block diagram of PCM which represents the basic elements of both the transmitter and the receiver sections.
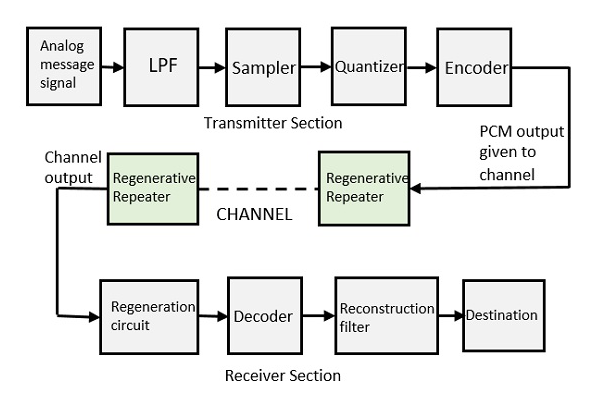
Low Pass Filter
This filter eliminates the high frequency components present in the input analog signal which is greater than the highest frequency of the message signal, to avoid aliasing of the message signal.
Sampler
This is the technique which helps to collect the sample data at instantaneous values of message signal, so as to reconstruct the original signal. The sampling rate must be greater than twice the highest frequency component W of the message signal, in accordance with the sampling theorem.
Quantizer
Quantizing is a process of reducing the excessive bits and confining the data. The sampled output when given to Quantizer, reduces the redundant bits and compresses the value.
Encoder
The digitization of analog signal is done by the encoder. It designates each quantized level by a binary code. The sampling done here is the sample-and-hold process. These three sections (LPF, Sampler, and Quantizer) will act as an analog to digital converter. Encoding minimizes the bandwidth used.
Regenerative Repeater
This section increases the signal strength. The output of the channel also has one regenerative repeater circuit, to compensate the signal loss and reconstruct the signal, and also to increase its strength.
Decoder
The decoder circuit decodes the pulse coded waveform to reproduce the original signal. This circuit acts as the demodulator.
Reconstruction Filter
After the digital-to-analog conversion is done by the regenerative circuit and the decoder, a low-pass filter is employed, called as the reconstruction filter to get back the original signal.
Hence, the Pulse Code Modulator circuit digitizes the given analog signal, codes it and samples it, and then transmits it in an analog form. This whole process is repeated in a reverse pattern to obtain the original signal.
Digital Communication - Sampling
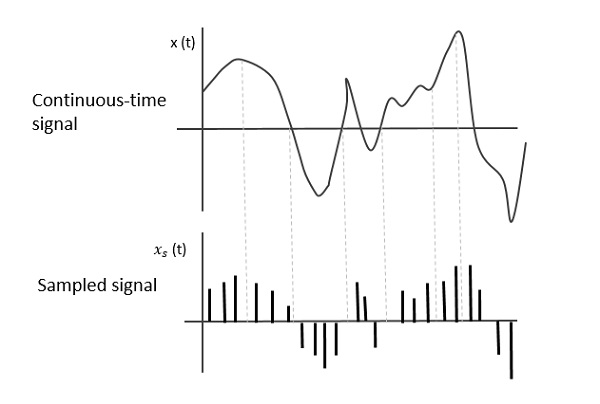
Sampling is defined as, The process of measuring the instantaneous values of continuous-time signal in a discrete form.
Sample is a piece of data taken from the whole data which is continuous in the time domain.
When a source generates an analog signal and if that has to be digitized, having 1s and 0s i.e., High or Low, the signal has to be discretized in time. This discretization of analog signal is called as Sampling.
The following figure indicates a continuous-time signal x (t) and a sampled signal xs (t). When x (t) is multiplied by a periodic impulse train, the sampled signal xs (t) is obtained.
Sampling Rate
To discretize the signals, the gap between the samples should be fixed. That gap can be termed as a sampling period Ts.
$$Sampling \: Frequency = \frac{1}{T_{s}} = f_s$$
Where,
$T_s$ is the sampling time
$f_s$ is the sampling frequency or the sampling rate
Sampling frequency is the reciprocal of the sampling period. This sampling frequency, can be simply called as Sampling rate. The sampling rate denotes the number of samples taken per second, or for a finite set of values.
For an analog signal to be reconstructed from the digitized signal, the sampling rate should be highly considered. The rate of sampling should be such that the data in the message signal should neither be lost nor it should get over-lapped. Hence, a rate was fixed for this, called as Nyquist rate.
Nyquist Rate
Suppose that a signal is band-limited with no frequency components higher than W Hertz. That means, W is the highest frequency. For such a signal, for effective reproduction of the original signal, the sampling rate should be twice the highest frequency.
Which means,
$$f_S = 2W$$
Where,
$f_S$ is the sampling rate
W is the highest frequency
This rate of sampling is called as Nyquist rate.
A theorem called, Sampling Theorem, was stated on the theory of this Nyquist rate.
Sampling Theorem
The sampling theorem, which is also called as Nyquist theorem, delivers the theory of sufficient sample rate in terms of bandwidth for the class of functions that are bandlimited.
The sampling theorem states that, a signal can be exactly reproduced if it is sampled at the rate fs which is greater than twice the maximum frequency W.
To understand this sampling theorem, let us consider a band-limited signal, i.e., a signal whose value is non-zero between some W and W Hertz.
Such a signal is represented as $x(f) = 0 \: for \: \mid f \mid > W$
For the continuous-time signal x (t), the band-limited signal in frequency domain, can be represented as shown in the following figure.
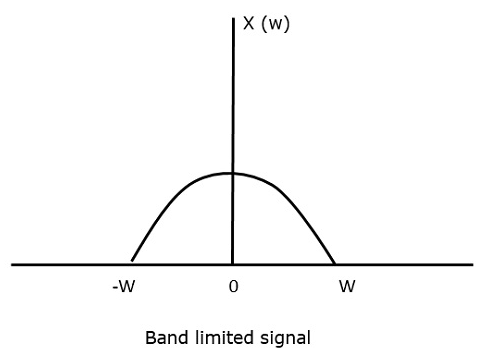
We need a sampling frequency, a frequency at which there should be no loss of information, even after sampling. For this, we have the Nyquist rate that the sampling frequency should be two times the maximum frequency. It is the critical rate of sampling.
If the signal x(t) is sampled above the Nyquist rate, the original signal can be recovered, and if it is sampled below the Nyquist rate, the signal cannot be recovered.
The following figure explains a signal, if sampled at a higher rate than 2w in the frequency domain.
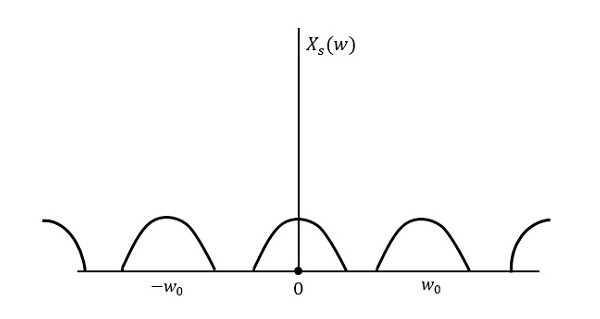
The above figure shows the Fourier transform of a signal xs (t). Here, the information is reproduced without any loss. There is no mixing up and hence recovery is possible.
The Fourier Transform of the signal xs (t) is
$$X_s(w) = \frac{1}{T_{s}}\sum_{n = - \infty}^\infty X(w-nw_0)$$
Where $T_s$ = Sampling Period and $w_0 = \frac{2 \pi}{T_s}$
Let us see what happens if the sampling rate is equal to twice the highest frequency (2W)
That means,
$$f_s = 2W$$
Where,
$f_s$ is the sampling frequency
W is the highest frequency
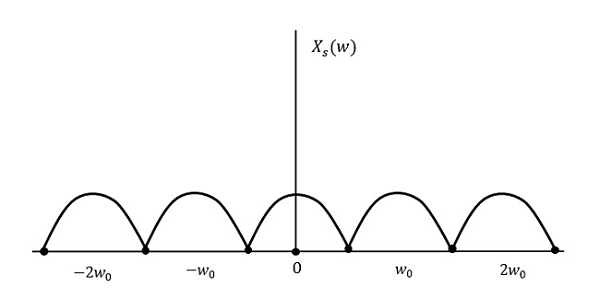
The result will be as shown in the above figure. The information is replaced without any loss. Hence, this is also a good sampling rate.
Now, let us look at the condition,
$$f_s < 2W$$
The resultant pattern will look like the following figure.
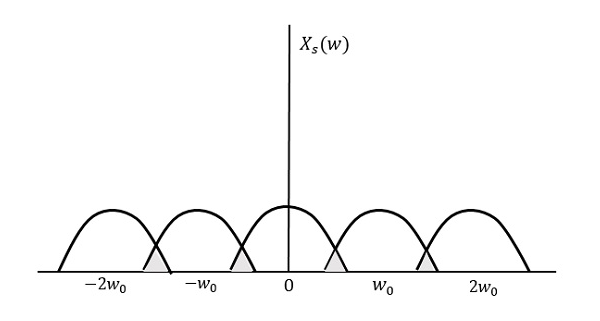
We can observe from the above pattern that the over-lapping of information is done, which leads to mixing up and loss of information. This unwanted phenomenon of over-lapping is called as Aliasing.
Aliasing
Aliasing can be referred to as the phenomenon of a high-frequency component in the spectrum of a signal, taking on the identity of a low-frequency component in the spectrum of its sampled version.
The corrective measures taken to reduce the effect of Aliasing are −
In the transmitter section of PCM, a low pass anti-aliasing filter is employed, before the sampler, to eliminate the high frequency components, which are unwanted.
The signal which is sampled after filtering, is sampled at a rate slightly higher than the Nyquist rate.
This choice of having the sampling rate higher than Nyquist rate, also helps in the easier design of the reconstruction filter at the receiver.
Scope of Fourier Transform
It is generally observed that, we seek the help of Fourier series and Fourier transforms in analyzing the signals and also in proving theorems. It is because −
The Fourier Transform is the extension of Fourier series for non-periodic signals.
Fourier transform is a powerful mathematical tool which helps to view the signals in different domains and helps to analyze the signals easily.
Any signal can be decomposed in terms of sum of sines and cosines using this Fourier transform.
In the next chapter, let us discuss about the concept of Quantization.
Digital Communication - Quantization
The digitization of analog signals involves the rounding off of the values which are approximately equal to the analog values. The method of sampling chooses a few points on the analog signal and then these points are joined to round off the value to a near stabilized value. Such a process is called as Quantization.
Quantizing an Analog Signal
The analog-to-digital converters perform this type of function to create a series of digital values out of the given analog signal. The following figure represents an analog signal. This signal to get converted into digital, has to undergo sampling and quantizing.
The quantizing of an analog signal is done by discretizing the signal with a number of quantization levels. Quantization is representing the sampled values of the amplitude by a finite set of levels, which means converting a continuous-amplitude sample into a discrete-time signal.
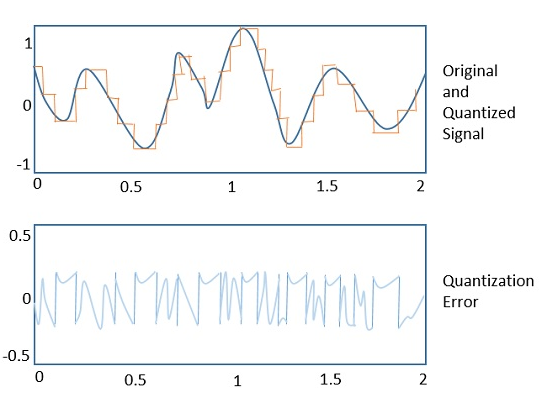
The following figure shows how an analog signal gets quantized. The blue line represents analog signal while the brown one represents the quantized signal.
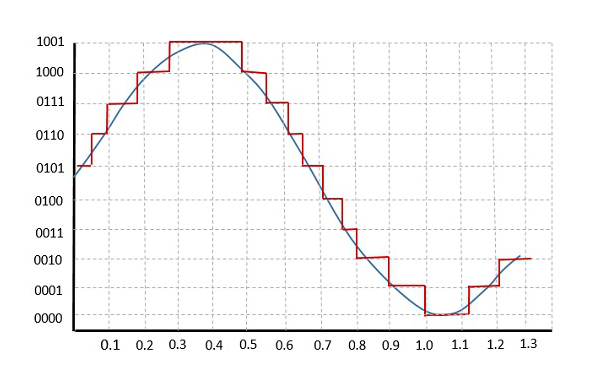
Both sampling and quantization result in the loss of information. The quality of a Quantizer output depends upon the number of quantization levels used. The discrete amplitudes of the quantized output are called as representation levels or reconstruction levels. The spacing between the two adjacent representation levels is called a quantum or step-size.
The following figure shows the resultant quantized signal which is the digital form for the given analog signal.
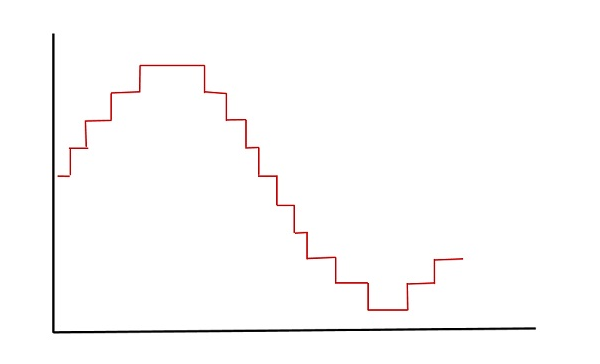
This is also called as Stair-case waveform, in accordance with its shape.
Types of Quantization
There are two types of Quantization - Uniform Quantization and Non-uniform Quantization.
The type of quantization in which the quantization levels are uniformly spaced is termed as a Uniform Quantization. The type of quantization in which the quantization levels are unequal and mostly the relation between them is logarithmic, is termed as a Non-uniform Quantization.
There are two types of uniform quantization. They are Mid-Rise type and Mid-Tread type. The following figures represent the two types of uniform quantization.
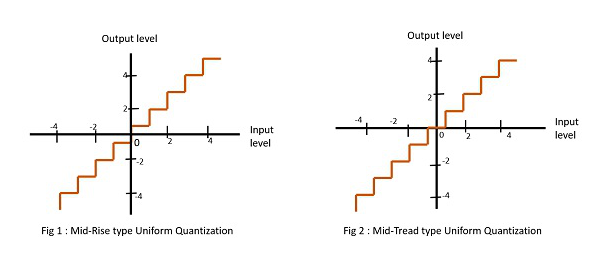
Figure 1 shows the mid-rise type and figure 2 shows the mid-tread type of uniform quantization.
The Mid-Rise type is so called because the origin lies in the middle of a raising part of the stair-case like graph. The quantization levels in this type are even in number.
The Mid-tread type is so called because the origin lies in the middle of a tread of the stair-case like graph. The quantization levels in this type are odd in number.
Both the mid-rise and mid-tread type of uniform quantizers are symmetric about the origin.
Quantization Error
For any system, during its functioning, there is always a difference in the values of its input and output. The processing of the system results in an error, which is the difference of those values.
The difference between an input value and its quantized value is called a Quantization Error. A Quantizer is a logarithmic function that performs Quantization (rounding off the value). An analog-to-digital converter (ADC) works as a quantizer.
The following figure illustrates an example for a quantization error, indicating the difference between the original signal and the quantized signal.
Quantization Noise
It is a type of quantization error, which usually occurs in analog audio signal, while quantizing it to digital. For example, in music, the signals keep changing continuously, where a regularity is not found in errors. Such errors create a wideband noise called as Quantization Noise.
Companding in PCM
The word Companding is a combination of Compressing and Expanding, which means that it does both. This is a non-linear technique used in PCM which compresses the data at the transmitter and expands the same data at the receiver. The effects of noise and crosstalk are reduced by using this technique.
There are two types of Companding techniques. They are −
A-law Companding Technique
Uniform quantization is achieved at A = 1, where the characteristic curve is linear and no compression is done.
A-law has mid-rise at the origin. Hence, it contains a non-zero value.
A-law companding is used for PCM telephone systems.
-law Companding Technique
Uniform quantization is achieved at = 0, where the characteristic curve is linear and no compression is done.
-law has mid-tread at the origin. Hence, it contains a zero value.
-law companding is used for speech and music signals.
-law is used in North America and Japan.
Digital Communication - Differential PCM
For the samples that are highly correlated, when encoded by PCM technique, leave redundant information behind. To process this redundant information and to have a better output, it is a wise decision to take a predicted sampled value, assumed from its previous output and summarize them with the quantized values. Such a process is called as Differential PCM (DPCM) technique.
DPCM Transmitter
The DPCM Transmitter consists of Quantizer and Predictor with two summer circuits. Following is the block diagram of DPCM transmitter.
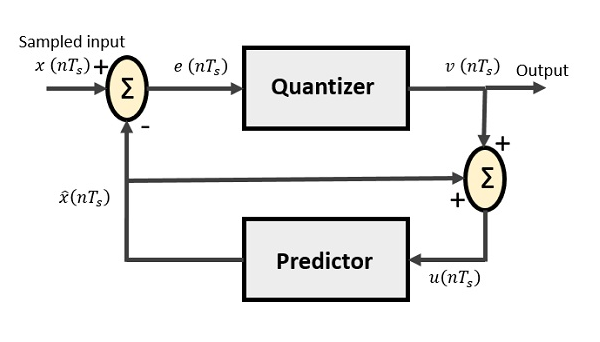
The signals at each point are named as −
$x(nT_s)$ is the sampled input
$\widehat{x}(nT_s)$ is the predicted sample
$e(nT_s)$ is the difference of sampled input and predicted output, often called as prediction error
$v(nT_s)$ is the quantized output
$u(nT_s)$ is the predictor input which is actually the summer output of the predictor output and the quantizer output
The predictor produces the assumed samples from the previous outputs of the transmitter circuit. The input to this predictor is the quantized versions of the input signal $x(nT_s)$.
Quantizer Output is represented as −
$$v(nT_s) = Q[e(nT_s)]$$
$= e(nT_s) + q(nT_s)$
Where q (nTs) is the quantization error
Predictor input is the sum of quantizer output and predictor output,
$$u(nT_s) = \widehat{x}(nT_s) + v(nT_s)$$
$u(nT_s) = \widehat{x}(nT_s) + e(nT_s) + q(nT_s)$
$$u(nT_s) = x(nT_s) + q(nT_s)$$
The same predictor circuit is used in the decoder to reconstruct the original input.
DPCM Receiver
The block diagram of DPCM Receiver consists of a decoder, a predictor, and a summer circuit. Following is the diagram of DPCM Receiver.
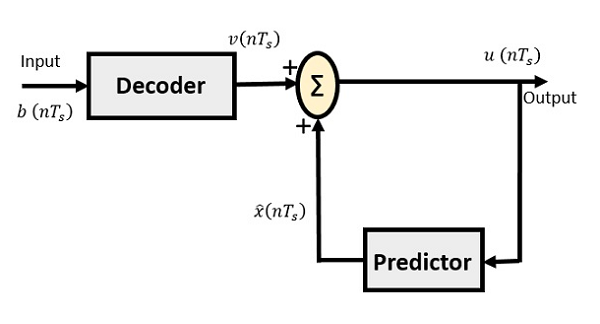
The notation of the signals is the same as the previous ones. In the absence of noise, the encoded receiver input will be the same as the encoded transmitter output.
As mentioned before, the predictor assumes a value, based on the previous outputs. The input given to the decoder is processed and that output is summed up with the output of the predictor, to obtain a better output.
Digital Communication - Delta Modulation
The sampling rate of a signal should be higher than the Nyquist rate, to achieve better sampling. If this sampling interval in Differential PCM is reduced considerably, the sampleto-sample amplitude difference is very small, as if the difference is 1-bit quantization, then the step-size will be very small i.e., Δ (delta).
Delta Modulation
The type of modulation, where the sampling rate is much higher and in which the stepsize after quantization is of a smaller value Δ, such a modulation is termed as delta modulation.
Features of Delta Modulation
Following are some of the features of delta modulation.
An over-sampled input is taken to make full use of the signal correlation.
The quantization design is simple.
The input sequence is much higher than the Nyquist rate.
The quality is moderate.
The design of the modulator and the demodulator is simple.
The stair-case approximation of output waveform.
The step-size is very small, i.e., Δ (delta).
The bit rate can be decided by the user.
This involves simpler implementation.
Delta Modulation is a simplified form of DPCM technique, also viewed as 1-bit DPCM scheme. As the sampling interval is reduced, the signal correlation will be higher.
Delta Modulator
The Delta Modulator comprises of a 1-bit quantizer and a delay circuit along with two summer circuits. Following is the block diagram of a delta modulator.
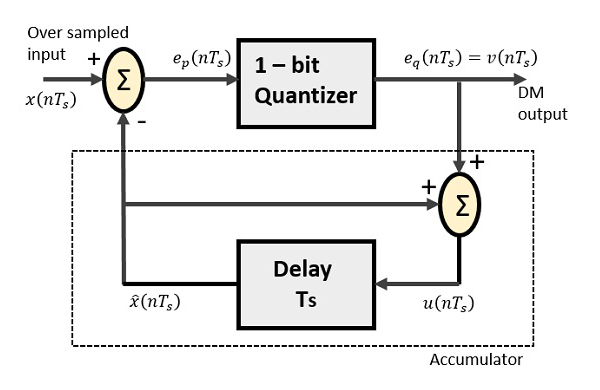
The predictor circuit in DPCM is replaced by a simple delay circuit in DM.
From the above diagram, we have the notations as −
$x(nT_s)$ = over sampled input
$e_p(nT_s)$ = summer output and quantizer input
$e_q(nT_s)$ = quantizer output = $v(nT_s)$
$\widehat{x}(nT_s)$ = output of delay circuit
$u(nT_s)$ = input of delay circuit
Using these notations, now we shall try to figure out the process of delta modulation.
$e_p(nT_s) = x(nT_s) - \widehat{x}(nT_s)$
---------equation 1
$= x(nT_s) - u([n - 1]T_s)$
$= x(nT_s) - [\widehat{x} [[n - 1]T_s] + v[[n-1]T_s]]$
---------equation 2
Further,
$v(nT_s) = e_q(nT_s) = S.sig.[e_p(nT_s)]$
---------equation 3
$u(nT_s) = \widehat{x}(nT_s)+e_q(nT_s)$
Where,
$\widehat{x}(nT_s)$ = the previous value of the delay circuit
$e_q(nT_s)$ = quantizer output = $v(nT_s)$
Hence,
$u(nT_s) = u([n-1]T_s) + v(nT_s)$
---------equation 4
Which means,
The present input of the delay unit
= (The previous output of the delay unit) + (the present quantizer output)
Assuming zero condition of Accumulation,
$u(nT_s) = S \displaystyle\sum\limits_{j=1}^n sig[e_p(jT_s)]$
Accumulated version of DM output = $\displaystyle\sum\limits_{j = 1}^n v(jT_s)$
---------equation 5
Now, note that
$\widehat{x}(nT_s) = u([n-1]T_s)$
$= \displaystyle\sum\limits_{j = 1}^{n - 1} v(jT_s)$
---------equation 6
Delay unit output is an Accumulator output lagging by one sample.
From equations 5 & 6, we get a possible structure for the demodulator.
A Stair-case approximated waveform will be the output of the delta modulator with the step-size as delta (Δ). The output quality of the waveform is moderate.
Delta Demodulator
The delta demodulator comprises of a low pass filter, a summer, and a delay circuit. The predictor circuit is eliminated here and hence no assumed input is given to the demodulator.
Following is the diagram for delta demodulator.
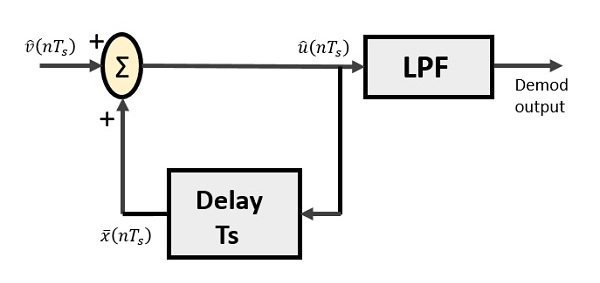
From the above diagram, we have the notations as −
$\widehat{v}(nT_s)$ is the input sample
$\widehat{u}(nT_s)$ is the summer output
$\bar{x}(nT_s)$ is the delayed output
A binary sequence will be given as an input to the demodulator. The stair-case approximated output is given to the LPF.
Low pass filter is used for many reasons, but the prominent reason is noise elimination for out-of-band signals. The step-size error that may occur at the transmitter is called granular noise, which is eliminated here. If there is no noise present, then the modulator output equals the demodulator input.
Advantages of DM Over DPCM
1-bit quantizer
Very easy design of the modulator and the demodulator
However, there exists some noise in DM.
Slope Over load distortion (when Δ is small)
Granular noise (when Δ is large)
Adaptive Delta Modulation (ADM)
In digital modulation, we have come across certain problem of determining the step-size, which influences the quality of the output wave.
A larger step-size is needed in the steep slope of modulating signal and a smaller stepsize is needed where the message has a small slope. The minute details get missed in the process. So, it would be better if we can control the adjustment of step-size, according to our requirement in order to obtain the sampling in a desired fashion. This is the concept of Adaptive Delta Modulation.
Following is the block diagram of Adaptive delta modulator.
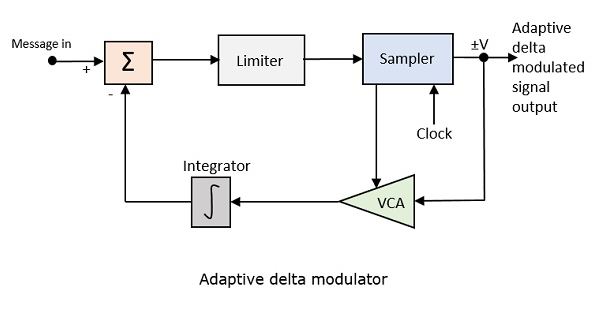
The gain of the voltage controlled amplifier is adjusted by the output signal from the sampler. The amplifier gain determines the step-size and both are proportional.
ADM quantizes the difference between the value of the current sample and the predicted value of the next sample. It uses a variable step height to predict the next values, for the faithful reproduction of the fast varying values.
Digital Communication - Techniques
There are a few techniques which have paved the basic path to digital communication processes. For the signals to get digitized, we have the sampling and quantizing techniques.
For them to be represented mathematically, we have LPC and digital multiplexing techniques. These digital modulation techniques are further discussed.
Linear Predictive Coding
Linear Predictive Coding (LPC) is a tool which represents digital speech signals in linear predictive model. This is mostly used in audio signal processing, speech synthesis, speech recognition, etc.
Linear prediction is based on the idea that the current sample is based on the linear combination of past samples. The analysis estimates the values of a discrete-time signal as a linear function of the previous samples.
The spectral envelope is represented in a compressed form, using the information of the linear predictive model. This can be mathematically represented as −
$s(n) = \displaystyle\sum\limits_{k = 1}^p \alpha_k s(n - k)$ for some value of p and αk
Where
s(n) is the current speech sample
k is a particular sample
p is the most recent value
αk is the predictor co-efficient
s(n - k) is the previous speech sample
For LPC, the predictor co-efficient values are determined by minimizing the sum of squared differences (over a finite interval) between the actual speech samples and the linearly predicted ones.
This is a very useful method for encoding speech at a low bit rate. The LPC method is very close to the Fast Fourier Transform (FFT) method.
Multiplexing
Multiplexing is the process of combining multiple signals into one signal, over a shared medium. These signals, if analog in nature, the process is called as analog multiplexing. If digital signals are multiplexed, it is called as digital multiplexing.
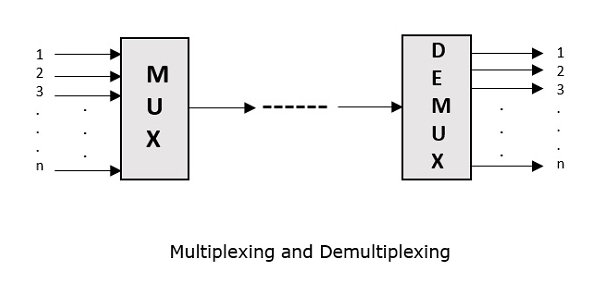
Multiplexing was first developed in telephony. A number of signals were combined to send through a single cable. The process of multiplexing divides a communication channel into several number of logical channels, allotting each one for a different message signal or a data stream to be transferred. The device that does multiplexing, can be called as a MUX. The reverse process, i.e., extracting the number of channels from one, which is done at the receiver is called as de-multiplexing. The device which does de-multiplexing is called as DEMUX.
The following figures represent MUX and DEMUX. Their primary use is in the field of communications.
Types of Multiplexers
There are mainly two types of multiplexers, namely analog and digital. They are further divided into FDM, WDM, and TDM. The following figure gives a detailed idea on this classification.
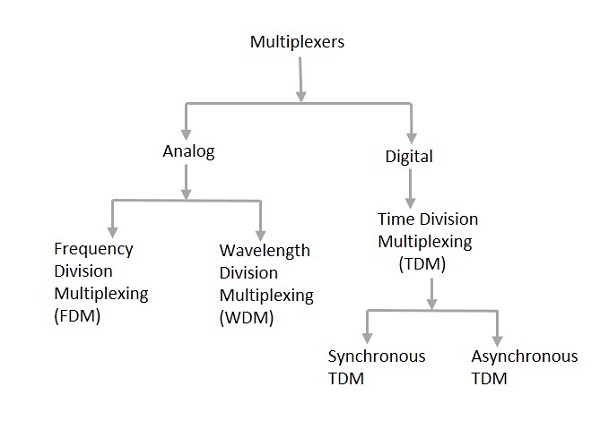
Actually, there are many types of multiplexing techniques. Of them all, we have the main types with general classification, mentioned in the above figure.
Analog Multiplexing
The analog multiplexing techniques involve signals which are analog in nature. The analog signals are multiplexed according to their frequency (FDM) or wavelength (WDM).
Frequency Division Multiplexing (FDM)
In analog multiplexing, the most used technique is Frequency Division Multiplexing (FDM). This technique uses various frequencies to combine streams of data, for sending them on a communication medium, as a single signal.
Example − A traditional television transmitter, which sends a number of channels through a single cable, uses FDM.
Wavelength Division Multiplexing (WDM)
Wavelength Division multiplexing is an analog technique, in which many data streams of different wavelengths are transmitted in the light spectrum. If the wavelength increases, the frequency of the signal decreases. A prism which can turn different wavelengths into a single line, can be used at the output of MUX and input of DEMUX.
Example − Optical fiber communications use WDM technique to merge different wavelengths into a single light for communication.
Digital Multiplexing
The term digital represents the discrete bits of information. Hence, the available data is in the form of frames or packets, which are discrete.
Time Division Multiplexing (TDM)
In TDM, the time frame is divided into slots. This technique is used to transmit a signal over a single communication channel, by allotting one slot for each message.
Of all the types of TDM, the main ones are Synchronous and Asynchronous TDM.
Synchronous TDM
In Synchronous TDM, the input is connected to a frame. If there are n number of connections, then the frame is divided into n time slots. One slot is allocated for each input line.
In this technique, the sampling rate is common to all signals and hence the same clock input is given. The MUX allocates the same slot to each device at all times.
Asynchronous TDM
In Asynchronous TDM, the sampling rate is different for each of the signals and a common clock is not required. If the allotted device, for a time-slot, transmits nothing and sits idle, then that slot is allotted to another device, unlike synchronous. This type of TDM is used in Asynchronous transfer mode networks.
Regenerative Repeater
For any communication system to be reliable, it should transmit and receive the signals effectively, without any loss. A PCM wave, after transmitting through a channel, gets distorted due to the noise introduced by the channel.
The regenerative pulse compared with the original and received pulse, will be as shown in the following figure.
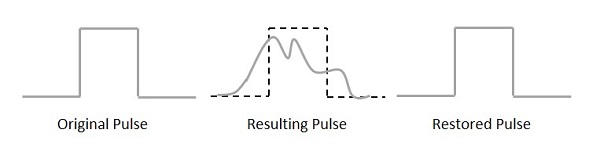
For a better reproduction of the signal, a circuit called as regenerative repeater is employed in the path before the receiver. This helps in restoring the signals from the losses occurred. Following is the diagrammatical representation.
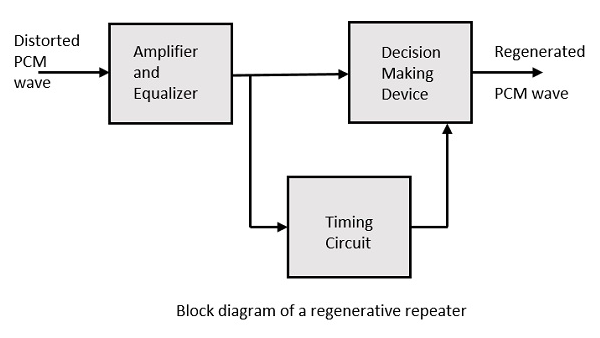
This consists of an equalizer along with an amplifier, a timing circuit, and a decision making device. Their working of each of the components is detailed as follows.
Equalizer
The channel produces amplitude and phase distortions to the signals. This is due to the transmission characteristics of the channel. The Equalizer circuit compensates these losses by shaping the received pulses.
Timing Circuit
To obtain a quality output, the sampling of the pulses should be done where the signal to noise ratio (SNR) is maximum. To achieve this perfect sampling, a periodic pulse train has to be derived from the received pulses, which is done by the timing circuit.
Hence, the timing circuit, allots the timing interval for sampling at high SNR, through the received pulses.
Decision Device
The timing circuit determines the sampling times. The decision device is enabled at these sampling times. The decision device decides its output based on whether the amplitude of the quantized pulse and the noise, exceeds a pre-determined value or not.
These are few of the techniques used in digital communications. There are other important techniques to be learned, called as data encoding techniques. Let us learn about them in the subsequent chapters, after taking a look at the line codes.
Digital Communication - Line Codes
A line code is the code used for data transmission of a digital signal over a transmission line. This process of coding is chosen so as to avoid overlap and distortion of signal such as inter-symbol interference.
Properties of Line Coding
Following are the properties of line coding −
As the coding is done to make more bits transmit on a single signal, the bandwidth used is much reduced.
For a given bandwidth, the power is efficiently used.
The probability of error is much reduced.
Error detection is done and the bipolar too has a correction capability.
Power density is much favorable.
The timing content is adequate.
Long strings of 1s and 0s is avoided to maintain transparency.
Types of Line Coding
There are 3 types of Line Coding
- Unipolar
- Polar
- Bi-polar
Unipolar Signaling
Unipolar signaling is also called as On-Off Keying or simply OOK.
The presence of pulse represents a 1 and the absence of pulse represents a 0.
There are two variations in Unipolar signaling −
- Non Return to Zero (NRZ)
- Return to Zero (RZ)
Unipolar Non-Return to Zero (NRZ)
In this type of unipolar signaling, a High in data is represented by a positive pulse called as Mark, which has a duration T0 equal to the symbol bit duration. A Low in data input has no pulse.
The following figure clearly depicts this.
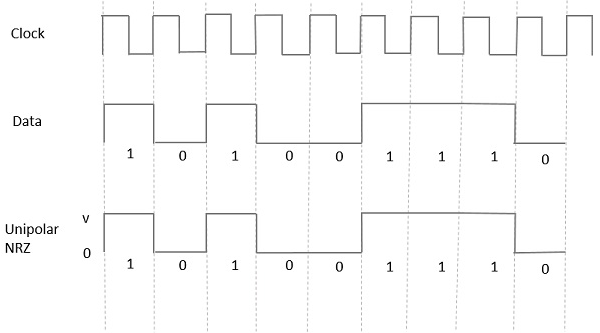
Advantages
The advantages of Unipolar NRZ are −
- It is simple.
- A lesser bandwidth is required.
Disadvantages
The disadvantages of Unipolar NRZ are −
No error correction done.
Presence of low frequency components may cause the signal droop.
No clock is present.
Loss of synchronization is likely to occur (especially for long strings of 1s and 0s).
Unipolar Return to Zero (RZ)
In this type of unipolar signaling, a High in data, though represented by a Mark pulse, its duration T0 is less than the symbol bit duration. Half of the bit duration remains high but it immediately returns to zero and shows the absence of pulse during the remaining half of the bit duration.
It is clearly understood with the help of the following figure.
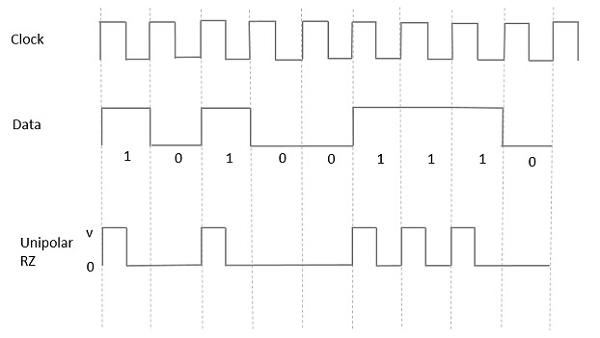
Advantages
The advantages of Unipolar RZ are −
- It is simple.
- The spectral line present at the symbol rate can be used as a clock.
Disadvantages
The disadvantages of Unipolar RZ are −
- No error correction.
- Occupies twice the bandwidth as unipolar NRZ.
- The signal droop is caused at the places where signal is non-zero at 0 Hz.
Polar Signaling
There are two methods of Polar Signaling. They are −
- Polar NRZ
- Polar RZ
Polar NRZ
In this type of Polar signaling, a High in data is represented by a positive pulse, while a Low in data is represented by a negative pulse. The following figure depicts this well.
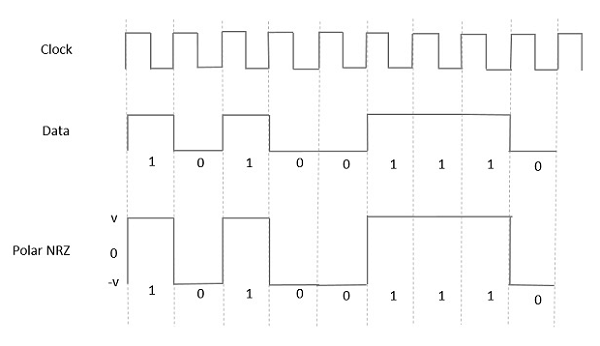
Advantages
The advantages of Polar NRZ are −
- It is simple.
- No low-frequency components are present.
Disadvantages
The disadvantages of Polar NRZ are −
No error correction.
No clock is present.
The signal droop is caused at the places where the signal is non-zero at 0 Hz.
Polar RZ
In this type of Polar signaling, a High in data, though represented by a Mark pulse, its duration T0 is less than the symbol bit duration. Half of the bit duration remains high but it immediately returns to zero and shows the absence of pulse during the remaining half of the bit duration.
However, for a Low input, a negative pulse represents the data, and the zero level remains same for the other half of the bit duration. The following figure depicts this clearly.
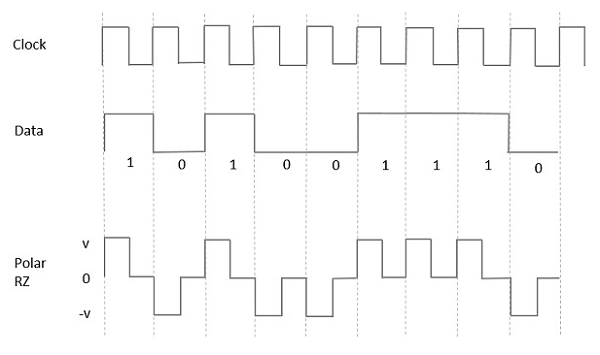
Advantages
The advantages of Polar RZ are −
- It is simple.
- No low-frequency components are present.
Disadvantages
The disadvantages of Polar RZ are −
No error correction.
No clock is present.
Occupies twice the bandwidth of Polar NRZ.
The signal droop is caused at places where the signal is non-zero at 0 Hz.
Bipolar Signaling
This is an encoding technique which has three voltage levels namely +, - and 0. Such a signal is called as duo-binary signal.
An example of this type is Alternate Mark Inversion (AMI). For a 1, the voltage level gets a transition from + to or from to +, having alternate 1s to be of equal polarity. A 0 will have a zero voltage level.
Even in this method, we have two types.
- Bipolar NRZ
- Bipolar RZ
From the models so far discussed, we have learnt the difference between NRZ and RZ. It just goes in the same way here too. The following figure clearly depicts this.
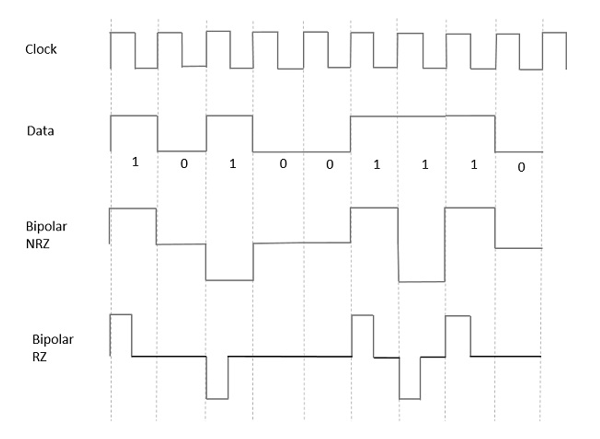
The above figure has both the Bipolar NRZ and RZ waveforms. The pulse duration and symbol bit duration are equal in NRZ type, while the pulse duration is half of the symbol bit duration in RZ type.
Advantages
Following are the advantages −
It is simple.
No low-frequency components are present.
Occupies low bandwidth than unipolar and polar NRZ schemes.
This technique is suitable for transmission over AC coupled lines, as signal drooping doesnt occur here.
A single error detection capability is present in this.
Disadvantages
Following are the disadvantages −
- No clock is present.
- Long strings of data causes loss of synchronization.
Power Spectral Density
The function which describes how the power of a signal got distributed at various frequencies, in the frequency domain is called as Power Spectral Density (PSD).
PSD is the Fourier Transform of Auto-Correlation (Similarity between observations). It is in the form of a rectangular pulse.
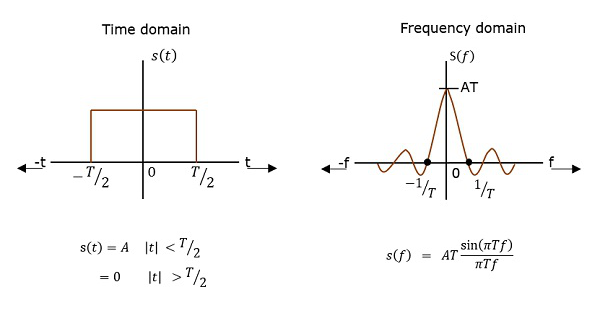
PSD Derivation
According to the Einstein-Wiener-Khintchine theorem, if the auto correlation function or power spectral density of a random process is known, the other can be found exactly.
Hence, to derive the power spectral density, we shall use the time auto-correlation $(R_x(\tau))$ of a power signal $x(t)$ as shown below.
$R_x(\tau) = \lim_{T_p \rightarrow \infty}\frac{1}{T_p}\int_{\frac{{-T_p}}{2}}^{\frac{T_p}{2}}x(t)x(t + \tau)dt$
Since $x(t)$ consists of impulses, $R_x(\tau)$ can be written as
$R_x(\tau) = \frac{1}{T}\displaystyle\sum\limits_{n = -\infty}^\infty R_n\delta(\tau - nT)$
Where $R_n = \lim_{N \rightarrow \infty}\frac{1}{N}\sum_ka_ka_{k + n}$
Getting to know that $R_n = R_{-n}$ for real signals, we have
$S_x(w) = \frac{1}{T}(R_0 + 2\displaystyle\sum\limits_{n = 1}^\infty R_n \cos nwT)$
Since the pulse filter has the spectrum of $(w) \leftrightarrow f(t)$, we have
$s_y(w) = \mid F(w) \mid^2S_x(w)$
$= \frac{\mid F(w) \mid^2}{T}(\displaystyle\sum\limits_{n = -\infty}^\infty R_ne^{-jnwT_{b}})$
$= \frac{\mid F(w) \mid^2}{T}(R_0 + 2\displaystyle\sum\limits_{n = 1}^\infty R_n \cos nwT)$
Hence, we get the equation for Power Spectral Density. Using this, we can find the PSD of various line codes.
Data Encoding Techniques
Encoding is the process of converting the data or a given sequence of characters, symbols, alphabets etc., into a specified format, for the secured transmission of data. Decoding is the reverse process of encoding which is to extract the information from the converted format.
Data Encoding
Encoding is the process of using various patterns of voltage or current levels to represent 1s and 0s of the digital signals on the transmission link.
The common types of line encoding are Unipolar, Polar, Bipolar, and Manchester.
Encoding Techniques
The data encoding technique is divided into the following types, depending upon the type of data conversion.
Analog data to Analog signals − The modulation techniques such as Amplitude Modulation, Frequency Modulation and Phase Modulation of analog signals, fall under this category.
Analog data to Digital signals − This process can be termed as digitization, which is done by Pulse Code Modulation (PCM). Hence, it is nothing but digital modulation. As we have already discussed, sampling and quantization are the important factors in this. Delta Modulation gives a better output than PCM.
Digital data to Analog signals − The modulation techniques such as Amplitude Shift Keying (ASK), Frequency Shift Keying (FSK), Phase Shift Keying (PSK), etc., fall under this category. These will be discussed in subsequent chapters.
Digital data to Digital signals − These are in this section. There are several ways to map digital data to digital signals. Some of them are −
Non Return to Zero (NRZ)
NRZ Codes has 1 for High voltage level and 0 for Low voltage level. The main behavior of NRZ codes is that the voltage level remains constant during bit interval. The end or start of a bit will not be indicated and it will maintain the same voltage state, if the value of the previous bit and the value of the present bit are same.
The following figure explains the concept of NRZ coding.
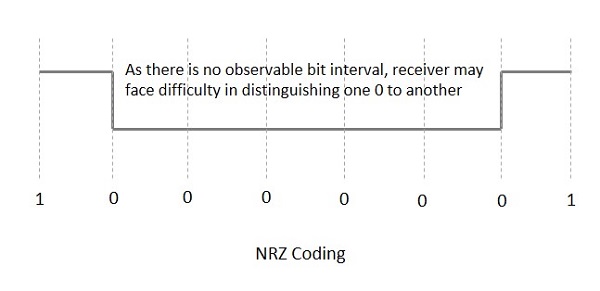
If the above example is considered, as there is a long sequence of constant voltage level and the clock synchronization may be lost due to the absence of bit interval, it becomes difficult for the receiver to differentiate between 0 and 1.
There are two variations in NRZ namely −
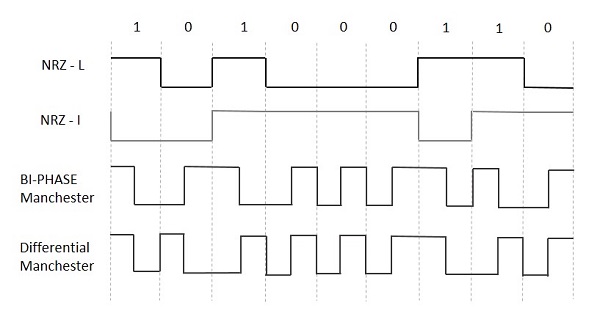
NRZ - L (NRZ LEVEL)
There is a change in the polarity of the signal, only when the incoming signal changes from 1 to 0 or from 0 to 1. It is the same as NRZ, however, the first bit of the input signal should have a change of polarity.
NRZ - I (NRZ INVERTED)
If a 1 occurs at the incoming signal, then there occurs a transition at the beginning of the bit interval. For a 0 at the incoming signal, there is no transition at the beginning of the bit interval.
NRZ codes has a disadvantage that the synchronization of the transmitter clock with the receiver clock gets completely disturbed, when there is a string of 1s and 0s. Hence, a separate clock line needs to be provided.
Bi-phase Encoding
The signal level is checked twice for every bit time, both initially and in the middle. Hence, the clock rate is double the data transfer rate and thus the modulation rate is also doubled. The clock is taken from the signal itself. The bandwidth required for this coding is greater.
There are two types of Bi-phase Encoding.
- Bi-phase Manchester
- Differential Manchester
Bi-phase Manchester
In this type of coding, the transition is done at the middle of the bit-interval. The transition for the resultant pulse is from High to Low in the middle of the interval, for the input bit 1. While the transition is from Low to High for the input bit 0.
Differential Manchester
In this type of coding, there always occurs a transition in the middle of the bit interval. If there occurs a transition at the beginning of the bit interval, then the input bit is 0. If no transition occurs at the beginning of the bit interval, then the input bit is 1.
The following figure illustrates the waveforms of NRZ-L, NRZ-I, Bi-phase Manchester and Differential Manchester coding for different digital inputs.
Block Coding
Among the types of block coding, the famous ones are 4B/5B encoding and 8B/6T encoding. The number of bits are processed in different manners, in both of these processes.
4B/5B Encoding
In Manchester encoding, to send the data, the clocks with double speed is required rather than NRZ coding. Here, as the name implies, 4 bits of code is mapped with 5 bits, with a minimum number of 1 bits in the group.
The clock synchronization problem in NRZ-I encoding is avoided by assigning an equivalent word of 5 bits in the place of each block of 4 consecutive bits. These 5-bit words are predetermined in a dictionary.
The basic idea of selecting a 5-bit code is that, it should have one leading 0 and it should have no more than two trailing 0s. Hence, these words are chosen such that two transactions take place per block of bits.
8B/6T Encoding
We have used two voltage levels to send a single bit over a single signal. But if we use more than 3 voltage levels, we can send more bits per signal.
For example, if 6 voltage levels are used to represent 8 bits on a single signal, then such encoding is termed as 8B/6T encoding. Hence in this method, we have as many as 729 (3^6) combinations for signal and 256 (2^8) combinations for bits.
These are the techniques mostly used for converting digital data into digital signals by compressing or coding them for reliable transmission of data.
Digital Communication - Pulse Shaping
After going through different types of coding techniques, we have an idea on how the data is prone to distortion and how the measures are taken to prevent it from getting affected so as to establish a reliable communication.
There is another important distortion which is most likely to occur, called as Inter-Symbol Interference (ISI).
Inter Symbol Interference
This is a form of distortion of a signal, in which one or more symbols interfere with subsequent signals, causing noise or delivering a poor output.
Causes of ISI
The main causes of ISI are −
- Multi-path Propagation
- Non-linear frequency in channels
The ISI is unwanted and should be completely eliminated to get a clean output. The causes of ISI should also be resolved in order to lessen its effect.
To view ISI in a mathematical form present in the receiver output, we can consider the receiver output.
The receiving filter output $y(t)$ is sampled at time $t_i = iT_b$ (with i taking on integer values), yielding −
$y(t_i) = \mu \displaystyle\sum\limits_{k = -\infty}^{\infty}a_kp(iT_b - kT_b)$
$= \mu a_i + \mu \displaystyle\sum\limits_{k = -\infty \\ k \neq i}^{\infty}a_kp(iT_b - kT_b)$
In the above equation, the first term $\mu a_i$ is produced by the ith transmitted bit.
The second term represents the residual effect of all other transmitted bits on the decoding of the ith bit. This residual effect is called as Inter Symbol Interference.
In the absence of ISI, the output will be −
$$y(t_i) = \mu a_i$$
This equation shows that the ith bit transmitted is correctly reproduced. However, the presence of ISI introduces bit errors and distortions in the output.
While designing the transmitter or a receiver, it is important that you minimize the effects of ISI, so as to receive the output with the least possible error rate.
Correlative Coding
So far, weve discussed that ISI is an unwanted phenomenon and degrades the signal. But the same ISI if used in a controlled manner, is possible to achieve a bit rate of 2W bits per second in a channel of bandwidth W Hertz. Such a scheme is called as Correlative Coding or Partial response signaling schemes.
Since the amount of ISI is known, it is easy to design the receiver according to the requirement so as to avoid the effect of ISI on the signal. The basic idea of correlative coding is achieved by considering an example of Duo-binary Signaling.
Duo-binary Signaling
The name duo-binary means doubling the binary systems transmission capability. To understand this, let us consider a binary input sequence {ak} consisting of uncorrelated binary digits each having a duration Ta seconds. In this, the signal 1 is represented by a +1 volt and the symbol 0 by a -1 volt.
Therefore, the duo-binary coder output ck is given as the sum of present binary digit ak and the previous value ak-1 as shown in the following equation.
$$c_k = a_k + a_{k-1}$$
The above equation states that the input sequence of uncorrelated binary sequence {ak} is changed into a sequence of correlated three level pulses {ck}. This correlation between the pulses may be understood as introducing ISI in the transmitted signal in an artificial manner.
Eye Pattern
An effective way to study the effects of ISI is the Eye Pattern. The name Eye Pattern was given from its resemblance to the human eye for binary waves. The interior region of the eye pattern is called the eye opening. The following figure shows the image of an eye-pattern.
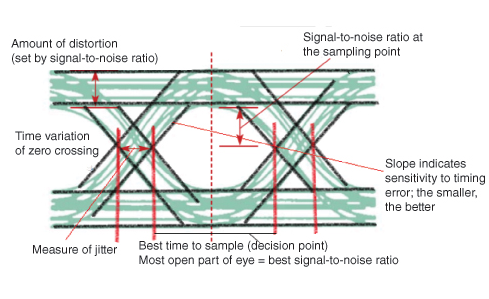
Jitter is the short-term variation of the instant of digital signal, from its ideal position, which may lead to data errors.
When the effect of ISI increases, traces from the upper portion to the lower portion of the eye opening increases and the eye gets completely closed, if ISI is very high.
An eye pattern provides the following information about a particular system.
Actual eye patterns are used to estimate the bit error rate and the signal-to-noise ratio.
The width of the eye opening defines the time interval over which the received wave can be sampled without error from ISI.
The instant of time when the eye opening is wide, will be the preferred time for sampling.
The rate of the closure of the eye, according to the sampling time, determines how sensitive the system is to the timing error.
The height of the eye opening, at a specified sampling time, defines the margin over noise.
Hence, the interpretation of eye pattern is an important consideration.
Equalization
For reliable communication to be established, we need to have a quality output. The transmission losses of the channel and other factors affecting the quality of the signal, have to be treated. The most occurring loss, as we have discussed, is the ISI.
To make the signal free from ISI, and to ensure a maximum signal to noise ratio, we need to implement a method called Equalization. The following figure shows an equalizer in the receiver portion of the communication system.
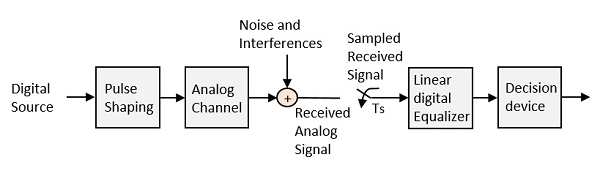
The noise and interferences which are denoted in the figure, are likely to occur, during transmission. The regenerative repeater has an equalizer circuit, which compensates the transmission losses by shaping the circuit. The Equalizer is feasible to get implemented.
Error Probability and Figure-of-merit
The rate at which data can be communicated is called the data rate. The rate at which error occurs in the bits, while transmitting data is called the Bit Error Rate (BER).
The probability of the occurrence of BER is the Error Probability. The increase in Signal to Noise Ratio (SNR) decreases the BER, hence the Error Probability also gets decreased.
In an Analog receiver, the figure of merit at the detection process can be termed as the ratio of output SNR to the input SNR. A greater value of figure-of-merit will be an advantage.
Digital Modulation Techniques
Digital-to-Analog signals is the next conversion we will discuss in this chapter. These techniques are also called as Digital Modulation techniques.
Digital Modulation provides more information capacity, high data security, quicker system availability with great quality communication. Hence, digital modulation techniques have a greater demand, for their capacity to convey larger amounts of data than analog modulation techniques.
There are many types of digital modulation techniques and also their combinations, depending upon the need. Of them all, we will discuss the prominent ones.
ASK Amplitude Shift Keying
The amplitude of the resultant output depends upon the input data whether it should be a zero level or a variation of positive and negative, depending upon the carrier frequency.
FSK Frequency Shift Keying
The frequency of the output signal will be either high or low, depending upon the input data applied.
PSK Phase Shift Keying
The phase of the output signal gets shifted depending upon the input. These are mainly of two types, namely Binary Phase Shift Keying (BPSK) and Quadrature Phase Shift Keying (QPSK), according to the number of phase shifts. The other one is Differential Phase Shift Keying (DPSK) which changes the phase according to the previous value.
M-ary Encoding
M-ary Encoding techniques are the methods where more than two bits are made to transmit simultaneously on a single signal. This helps in the reduction of bandwidth.
The types of M-ary techniques are −
- M-ary ASK
- M-ary FSK
- M-ary PSK
All of these are discussed in subsequent chapters.
Amplitude Shift Keying
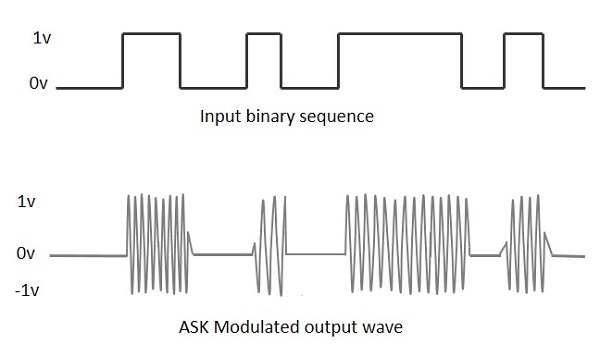
Amplitude Shift Keying (ASK) is a type of Amplitude Modulation which represents the binary data in the form of variations in the amplitude of a signal.
Any modulated signal has a high frequency carrier. The binary signal when ASK modulated, gives a zero value for Low input while it gives the carrier output for High input.
The following figure represents ASK modulated waveform along with its input.
To find the process of obtaining this ASK modulated wave, let us learn about the working of the ASK modulator.
ASK Modulator
The ASK modulator block diagram comprises of the carrier signal generator, the binary sequence from the message signal and the band-limited filter. Following is the block diagram of the ASK Modulator.
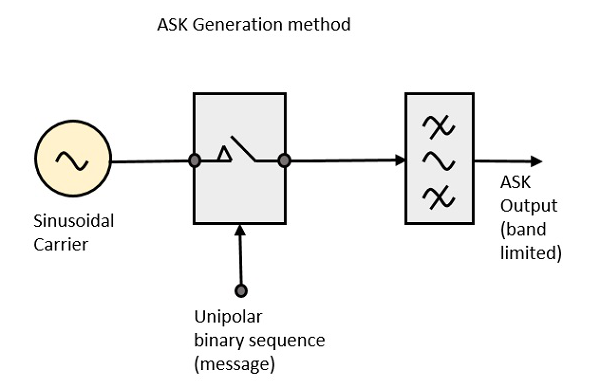
The carrier generator, sends a continuous high-frequency carrier. The binary sequence from the message signal makes the unipolar input to be either High or Low. The high signal closes the switch, allowing a carrier wave. Hence, the output will be the carrier signal at high input. When there is low input, the switch opens, allowing no voltage to appear. Hence, the output will be low.
The band-limiting filter, shapes the pulse depending upon the amplitude and phase characteristics of the band-limiting filter or the pulse-shaping filter.
ASK Demodulator
There are two types of ASK Demodulation techniques. They are −
- Asynchronous ASK Demodulation/detection
- Synchronous ASK Demodulation/detection
The clock frequency at the transmitter when matches with the clock frequency at the receiver, it is known as a Synchronous method, as the frequency gets synchronized. Otherwise, it is known as Asynchronous.
Asynchronous ASK Demodulator
The Asynchronous ASK detector consists of a half-wave rectifier, a low pass filter, and a comparator. Following is the block diagram for the same.
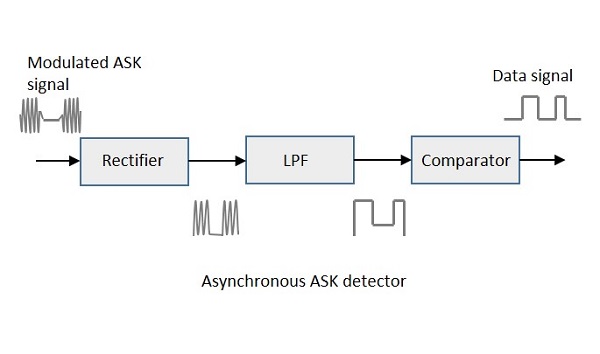
The modulated ASK signal is given to the half-wave rectifier, which delivers a positive half output. The low pass filter suppresses the higher frequencies and gives an envelope detected output from which the comparator delivers a digital output.
Synchronous ASK Demodulator
Synchronous ASK detector consists of a Square law detector, low pass filter, a comparator, and a voltage limiter. Following is the block diagram for the same.
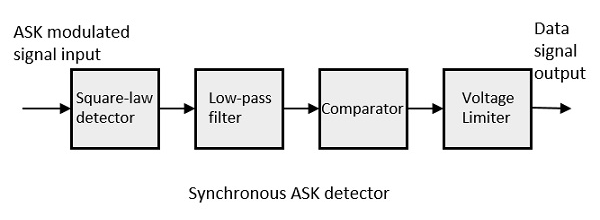
The ASK modulated input signal is given to the Square law detector. A square law detector is one whose output voltage is proportional to the square of the amplitude modulated input voltage. The low pass filter minimizes the higher frequencies. The comparator and the voltage limiter help to get a clean digital output.
Frequency Shift Keying
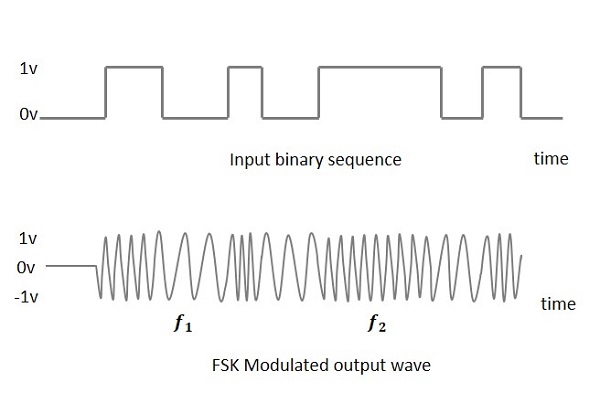
Frequency Shift Keying (FSK) is the digital modulation technique in which the frequency of the carrier signal varies according to the digital signal changes. FSK is a scheme of frequency modulation.
The output of a FSK modulated wave is high in frequency for a binary High input and is low in frequency for a binary Low input. The binary 1s and 0s are called Mark and Space frequencies.
The following image is the diagrammatic representation of FSK modulated waveform along with its input.
To find the process of obtaining this FSK modulated wave, let us know about the working of a FSK modulator.
FSK Modulator
The FSK modulator block diagram comprises of two oscillators with a clock and the input binary sequence. Following is its block diagram.
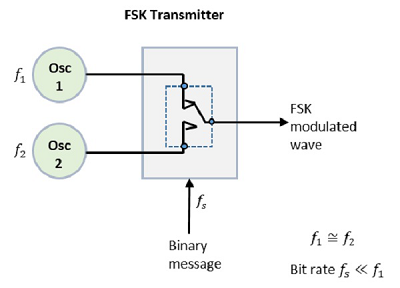
The two oscillators, producing a higher and a lower frequency signals, are connected to a switch along with an internal clock. To avoid the abrupt phase discontinuities of the output waveform during the transmission of the message, a clock is applied to both the oscillators, internally. The binary input sequence is applied to the transmitter so as to choose the frequencies according to the binary input.
FSK Demodulator
There are different methods for demodulating a FSK wave. The main methods of FSK detection are asynchronous detector and synchronous detector. The synchronous detector is a coherent one, while asynchronous detector is a non-coherent one.
Asynchronous FSK Detector
The block diagram of Asynchronous FSK detector consists of two band pass filters, two envelope detectors, and a decision circuit. Following is the diagrammatic representation.
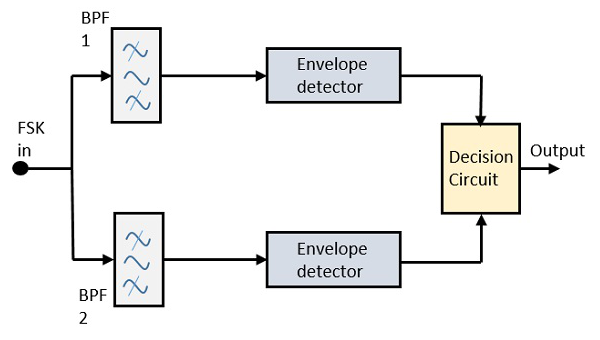
The FSK signal is passed through the two Band Pass Filters (BPFs), tuned to Space and Mark frequencies. The output from these two BPFs look like ASK signal, which is given to the envelope detector. The signal in each envelope detector is modulated asynchronously.
The decision circuit chooses which output is more likely and selects it from any one of the envelope detectors. It also re-shapes the waveform to a rectangular one.
Synchronous FSK Detector
The block diagram of Synchronous FSK detector consists of two mixers with local oscillator circuits, two band pass filters and a decision circuit. Following is the diagrammatic representation.
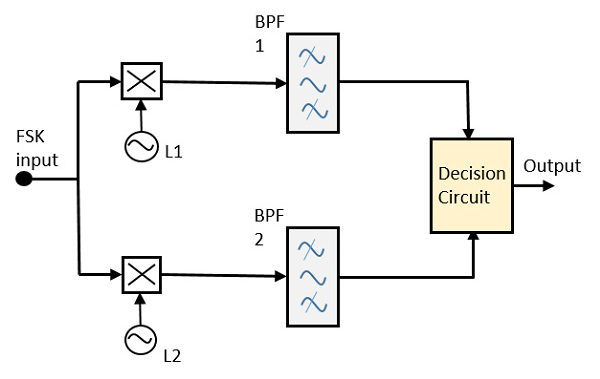
The FSK signal input is given to the two mixers with local oscillator circuits. These two are connected to two band pass filters. These combinations act as demodulators and the decision circuit chooses which output is more likely and selects it from any one of the detectors. The two signals have a minimum frequency separation.
For both of the demodulators, the bandwidth of each of them depends on their bit rate. This synchronous demodulator is a bit complex than asynchronous type demodulators.
Digital Communication - Phase Shift Keying
Phase Shift Keying (PSK) is the digital modulation technique in which the phase of the carrier signal is changed by varying the sine and cosine inputs at a particular time. PSK technique is widely used for wireless LANs, bio-metric, contactless operations, along with RFID and Bluetooth communications.
PSK is of two types, depending upon the phases the signal gets shifted. They are −
Binary Phase Shift Keying (BPSK)
This is also called as 2-phase PSK or Phase Reversal Keying. In this technique, the sine wave carrier takes two phase reversals such as 0° and 180°.
BPSK is basically a Double Side Band Suppressed Carrier (DSBSC) modulation scheme, for message being the digital information.
Quadrature Phase Shift Keying (QPSK)
This is the phase shift keying technique, in which the sine wave carrier takes four phase reversals such as 0°, 90°, 180°, and 270°.
If this kind of techniques are further extended, PSK can be done by eight or sixteen values also, depending upon the requirement.
BPSK Modulator
The block diagram of Binary Phase Shift Keying consists of the balance modulator which has the carrier sine wave as one input and the binary sequence as the other input. Following is the diagrammatic representation.
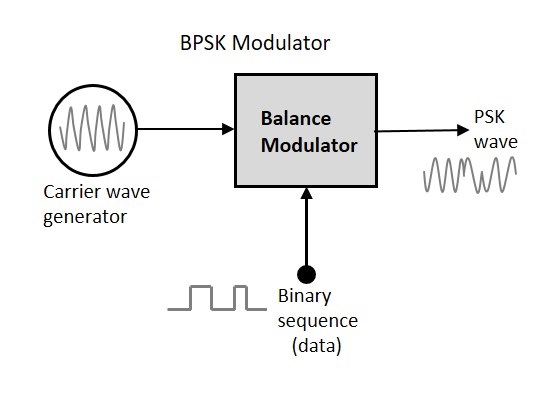
The modulation of BPSK is done using a balance modulator, which multiplies the two signals applied at the input. For a zero binary input, the phase will be 0° and for a high input, the phase reversal is of 180°.
Following is the diagrammatic representation of BPSK Modulated output wave along with its given input.
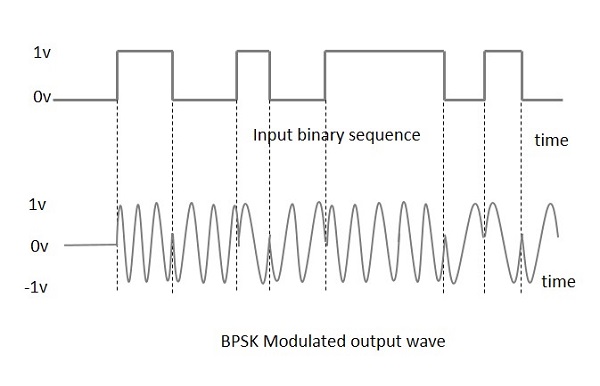
The output sine wave of the modulator will be the direct input carrier or the inverted (180° phase shifted) input carrier, which is a function of the data signal.
BPSK Demodulator
The block diagram of BPSK demodulator consists of a mixer with local oscillator circuit, a bandpass filter, a two-input detector circuit. The diagram is as follows.
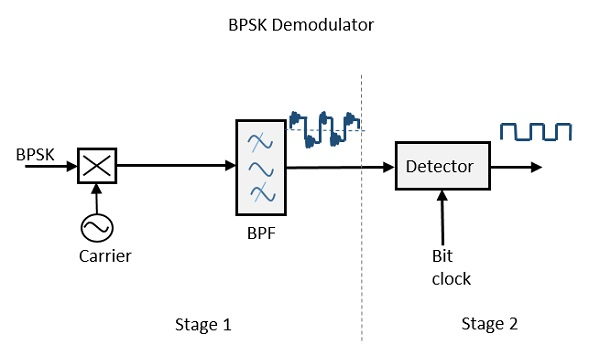
By recovering the band-limited message signal, with the help of the mixer circuit and the band pass filter, the first stage of demodulation gets completed. The base band signal which is band limited is obtained and this signal is used to regenerate the binary message bit stream.
In the next stage of demodulation, the bit clock rate is needed at the detector circuit to produce the original binary message signal. If the bit rate is a sub-multiple of the carrier frequency, then the bit clock regeneration is simplified. To make the circuit easily understandable, a decision-making circuit may also be inserted at the 2nd stage of detection.
Quadrature Phase Shift Keying
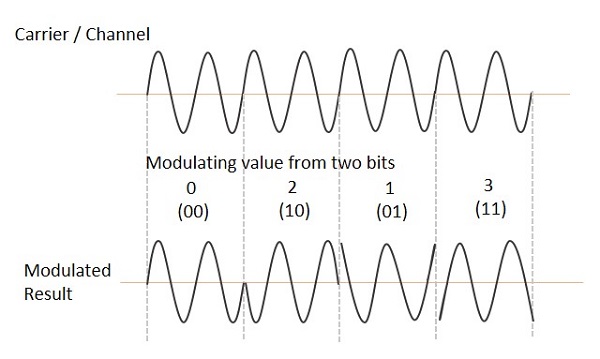
The Quadrature Phase Shift Keying (QPSK) is a variation of BPSK, and it is also a Double Side Band Suppressed Carrier (DSBSC) modulation scheme, which sends two bits of digital information at a time, called as bigits.
Instead of the conversion of digital bits into a series of digital stream, it converts them into bit pairs. This decreases the data bit rate to half, which allows space for the other users.
QPSK Modulator
The QPSK Modulator uses a bit-splitter, two multipliers with local oscillator, a 2-bit serial to parallel converter, and a summer circuit. Following is the block diagram for the same.
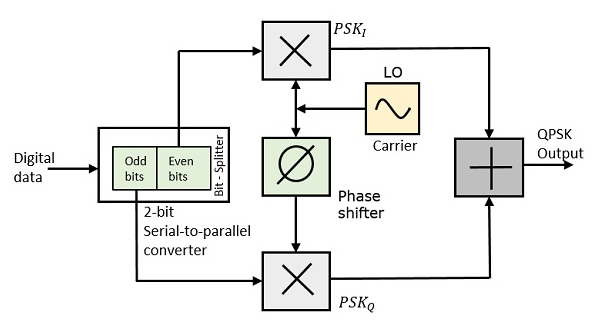
At the modulators input, the message signals even bits (i.e., 2nd bit, 4th bit, 6th bit, etc.) and odd bits (i.e., 1st bit, 3rd bit, 5th bit, etc.) are separated by the bits splitter and are multiplied with the same carrier to generate odd BPSK (called as PSKI) and even BPSK (called as PSKQ). The PSKQ signal is anyhow phase shifted by 90° before being modulated.
The QPSK waveform for two-bits input is as follows, which shows the modulated result for different instances of binary inputs.
QPSK Demodulator
The QPSK Demodulator uses two product demodulator circuits with local oscillator, two band pass filters, two integrator circuits, and a 2-bit parallel to serial converter. Following is the diagram for the same.
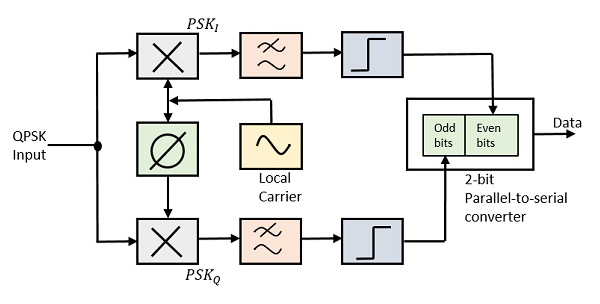
The two product detectors at the input of demodulator simultaneously demodulate the two BPSK signals. The pair of bits are recovered here from the original data. These signals after processing, are passed to the parallel to serial converter.
Differential Phase Shift Keying
In Differential Phase Shift Keying (DPSK) the phase of the modulated signal is shifted relative to the previous signal element. No reference signal is considered here. The signal phase follows the high or low state of the previous element. This DPSK technique doesnt need a reference oscillator.
The following figure represents the model waveform of DPSK.
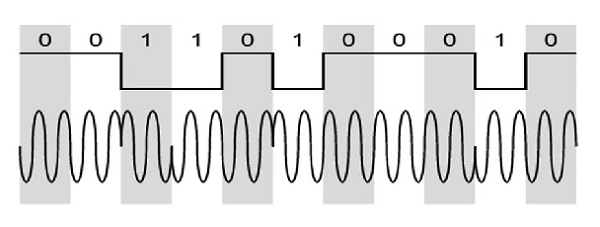
It is seen from the above figure that, if the data bit is Low i.e., 0, then the phase of the signal is not reversed, but continued as it was. If the data is a High i.e., 1, then the phase of the signal is reversed, as with NRZI, invert on 1 (a form of differential encoding).
If we observe the above waveform, we can say that the High state represents an M in the modulating signal and the Low state represents a W in the modulating signal.
DPSK Modulator
DPSK is a technique of BPSK, in which there is no reference phase signal. Here, the transmitted signal itself can be used as a reference signal. Following is the diagram of DPSK Modulator.
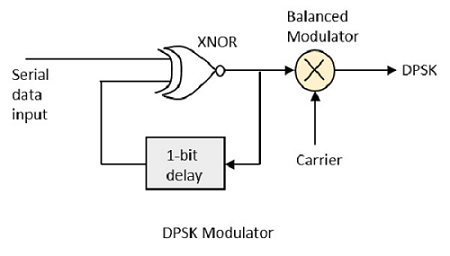
DPSK encodes two distinct signals, i.e., the carrier and the modulating signal with 180° phase shift each. The serial data input is given to the XNOR gate and the output is again fed back to the other input through 1-bit delay. The output of the XNOR gate along with the carrier signal is given to the balance modulator, to produce the DPSK modulated signal.
DPSK Demodulator
In DPSK demodulator, the phase of the reversed bit is compared with the phase of the previous bit. Following is the block diagram of DPSK demodulator.
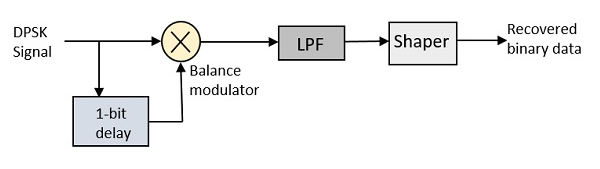
From the above figure, it is evident that the balance modulator is given the DPSK signal along with 1-bit delay input. That signal is made to confine to lower frequencies with the help of LPF. Then it is passed to a shaper circuit, which is a comparator or a Schmitt trigger circuit, to recover the original binary data as the output.
Digital Communication - M-ary Encoding
The word binary represents two bits. M represents a digit that corresponds to the number of conditions, levels, or combinations possible for a given number of binary variables.
This is the type of digital modulation technique used for data transmission in which instead of one bit, two or more bits are transmitted at a time. As a single signal is used for multiple bit transmission, the channel bandwidth is reduced.
M-ary Equation
If a digital signal is given under four conditions, such as voltage levels, frequencies, phases, and amplitude, then M = 4.
The number of bits necessary to produce a given number of conditions is expressed mathematically as
$$N = \log_{2}{M}$$
Where
N is the number of bits necessary
M is the number of conditions, levels, or combinations possible with N bits.
The above equation can be re-arranged as
$$2^N = M$$
For example, with two bits, 22 = 4 conditions are possible.
Types of M-ary Techniques
In general, Multi-level (M-ary) modulation techniques are used in digital communications as the digital inputs with more than two modulation levels are allowed on the transmitters input. Hence, these techniques are bandwidth efficient.
There are many M-ary modulation techniques. Some of these techniques, modulate one parameter of the carrier signal, such as amplitude, phase, and frequency.
M-ary ASK
This is called M-ary Amplitude Shift Keying (M-ASK) or M-ary Pulse Amplitude Modulation (PAM).
The amplitude of the carrier signal, takes on M different levels.
Representation of M-ary ASK
$S_m(t) = A_mcos (2 \pi f_ct) \quad A_m\epsilon {(2m - 1 - M) \Delta, m = 1,2... \: .M} \quad and \quad 0 \leq t \leq T_s$
Some prominent features of M-ary ASK are −
- This method is also used in PAM.
- Its implementation is simple.
- M-ary ASK is susceptible to noise and distortion.
M-ary FSK
This is called as M-ary Frequency Shift Keying (M-ary FSK).
The frequency of the carrier signal, takes on M different levels.
Representation of M-ary FSK
$S_i(t) = \sqrt{\frac{2E_s}{T_s}} \cos \left ( \frac{\pi}{T_s}\left (n_c+i\right )t\right )$ $0 \leq t \leq T_s \quad and \quad i = 1,2,3... \: ..M$
Where $f_c = \frac{n_c}{2T_s}$ for some fixed integer n.
Some prominent features of M-ary FSK are −
Not susceptible to noise as much as ASK.
The transmitted M number of signals are equal in energy and duration.
The signals are separated by $\frac{1}{2T_s}$ Hz making the signals orthogonal to each other.
Since M signals are orthogonal, there is no crowding in the signal space.
The bandwidth efficiency of M-ary FSK decreases and the power efficiency increases with the increase in M.
M-ary PSK
This is called as M-ary Phase Shift Keying (M-ary PSK).
The phase of the carrier signal, takes on M different levels.
Representation of M-ary PSK
$S_i(t) = \sqrt{\frac{2E}{T}} \cos \left (w_o t + \phi _it\right )$ $0 \leq t \leq T \quad and \quad i = 1,2 ... M$
$$\phi _i \left ( t \right ) = \frac{2 \pi i}{M} \quad where \quad i = 1,2,3 ... \: ...M$$
Some prominent features of M-ary PSK are −
The envelope is constant with more phase possibilities.
This method was used during the early days of space communication.
Better performance than ASK and FSK.
Minimal phase estimation error at the receiver.
The bandwidth efficiency of M-ary PSK decreases and the power efficiency increases with the increase in M.
So far, we have discussed different modulation techniques. The output of all these techniques is a binary sequence, represented as 1s and 0s. This binary or digital information has many types and forms, which are discussed further.
Digital Communication - Information Theory
Information is the source of a communication system, whether it is analog or digital. Information theory is a mathematical approach to the study of coding of information along with the quantification, storage, and communication of information.
Conditions of Occurrence of Events
If we consider an event, there are three conditions of occurrence.
If the event has not occurred, there is a condition of uncertainty.
If the event has just occurred, there is a condition of surprise.
If the event has occurred, a time back, there is a condition of having some information.
These three events occur at different times. The difference in these conditions help us gain knowledge on the probabilities of the occurrence of events.
Entropy
When we observe the possibilities of the occurrence of an event, how surprising or uncertain it would be, it means that we are trying to have an idea on the average content of the information from the source of the event.
Entropy can be defined as a measure of the average information content per source symbol. Claude Shannon, the father of the Information Theory, provided a formula for it as −
$$H = - \sum_{i} p_i \log_{b}p_i$$
Where pi is the probability of the occurrence of character number i from a given stream of characters and b is the base of the algorithm used. Hence, this is also called as Shannons Entropy.
The amount of uncertainty remaining about the channel input after observing the channel output, is called as Conditional Entropy. It is denoted by $H(x \mid y)$
Mutual Information
Let us consider a channel whose output is Y and input is X
Let the entropy for prior uncertainty be X = H(x)
(This is assumed before the input is applied)
To know about the uncertainty of the output, after the input is applied, let us consider Conditional Entropy, given that Y = yk
$$H\left ( x\mid y_k \right ) = \sum_{j = 0}^{j - 1}p\left ( x_j \mid y_k \right )\log_{2}\left [ \frac{1}{p(x_j \mid y_k)} \right ]$$
This is a random variable for $H(X \mid y = y_0) \: ... \: ... \: ... \: ... \: ... \: H(X \mid y = y_k)$ with probabilities $p(y_0) \: ... \: ... \: ... \: ... \: p(y_{k-1)}$ respectively.
The mean value of $H(X \mid y = y_k)$ for output alphabet y is −
$H\left ( X\mid Y \right ) = \displaystyle\sum\limits_{k = 0}^{k - 1}H\left ( X \mid y=y_k \right )p\left ( y_k \right )$
$= \displaystyle\sum\limits_{k = 0}^{k - 1} \displaystyle\sum\limits_{j = 0}^{j - 1}p\left (x_j \mid y_k \right )p\left ( y_k \right )\log_{2}\left [ \frac{1}{p\left ( x_j \mid y_k \right )} \right ]$
$= \displaystyle\sum\limits_{k = 0}^{k - 1} \displaystyle\sum\limits_{j = 0}^{j - 1}p\left (x_j ,y_k \right )\log_{2}\left [ \frac{1}{p\left ( x_j \mid y_k \right )} \right ]$
Now, considering both the uncertainty conditions (before and after applying the inputs), we come to know that the difference, i.e. $H(x) - H(x \mid y)$ must represent the uncertainty about the channel input that is resolved by observing the channel output.
This is called as the Mutual Information of the channel.
Denoting the Mutual Information as $I(x;y)$, we can write the whole thing in an equation, as follows
$$I(x;y) = H(x) - H(x \mid y)$$
Hence, this is the equational representation of Mutual Information.
Properties of Mutual information
These are the properties of Mutual information.
-
Mutual information of a channel is symmetric.
$$I(x;y) = I(y;x)$$
-
Mutual information is non-negative.
$$I(x;y) \geq 0$$
-
Mutual information can be expressed in terms of entropy of the channel output.
$$I(x;y) = H(y) - H(y \mid x)$$
Where $H(y \mid x)$ is a conditional entropy
-
Mutual information of a channel is related to the joint entropy of the channel input and the channel output.
$$I(x;y) = H(x)+H(y) - H(x,y)$$
Where the joint entropy $H(x,y)$ is defined by
$$H(x,y) = \displaystyle\sum\limits_{j=0}^{j-1} \displaystyle\sum\limits_{k=0}^{k-1}p(x_j,y_k)\log_{2} \left ( \frac{1}{p\left ( x_i,y_k \right )} \right )$$
Channel Capacity
We have so far discussed mutual information. The maximum average mutual information, in an instant of a signaling interval, when transmitted by a discrete memoryless channel, the probabilities of the rate of maximum reliable transmission of data, can be understood as the channel capacity.
It is denoted by C and is measured in bits per channel use.
Discrete Memoryless Source
A source from which the data is being emitted at successive intervals, which is independent of previous values, can be termed as discrete memoryless source.
This source is discrete as it is not considered for a continuous time interval, but at discrete time intervals. This source is memoryless as it is fresh at each instant of time, without considering the previous values.
Source Coding Theorem
The Code produced by a discrete memoryless source, has to be efficiently represented, which is an important problem in communications. For this to happen, there are code words, which represent these source codes.
For example, in telegraphy, we use Morse code, in which the alphabets are denoted by Marks and Spaces. If the letter E is considered, which is mostly used, it is denoted by . Whereas the letter Q which is rarely used, is denoted by --.-
Let us take a look at the block diagram.
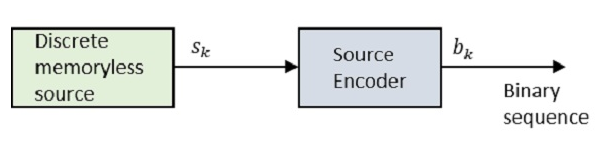
Where Sk is the output of the discrete memoryless source and bk is the output of the source encoder which is represented by 0s and 1s.
The encoded sequence is such that it is conveniently decoded at the receiver.
Let us assume that the source has an alphabet with k different symbols and that the kth symbol Sk occurs with the probability Pk, where k = 0, 1k-1.
Let the binary code word assigned to symbol Sk, by the encoder having length lk, measured in bits.
Hence, we define the average code word length L of the source encoder as
$$\overline{L} = \displaystyle\sum\limits_{k=0}^{k-1} p_kl_k$$
L represents the average number of bits per source symbol
If $L_{min} = \: minimum \: possible \: value \: of \: \overline{L}$
Then coding efficiency can be defined as
$$\eta = \frac{L{min}}{\overline{L}}$$
With $\overline{L}\geq L_{min}$ we will have $\eta \leq 1$
However, the source encoder is considered efficient when $\eta = 1$
For this, the value $L_{min}$ has to be determined.
Let us refer to the definition, Given a discrete memoryless source of entropy $H(\delta)$, the average code-word length L for any source encoding is bounded as $\overline{L} \geq H(\delta)$."
In simpler words, the code word (example: Morse code for the word QUEUE is -.- ..- . ..- . ) is always greater than or equal to the source code (QUEUE in example). Which means, the symbols in the code word are greater than or equal to the alphabets in the source code.
Hence with $L_{min} = H(\delta)$, the efficiency of the source encoder in terms of Entropy $H(\delta)$ may be written as
$$\eta = \frac{H(\delta)}{\overline{L}}$$
This source coding theorem is called as noiseless coding theorem as it establishes an error-free encoding. It is also called as Shannons first theorem.
Channel Coding Theorem
The noise present in a channel creates unwanted errors between the input and the output sequences of a digital communication system. The error probability should be very low, nearly ≤ 10-6 for a reliable communication.
The channel coding in a communication system, introduces redundancy with a control, so as to improve the reliability of the system. The source coding reduces redundancy to improve the efficiency of the system.
Channel coding consists of two parts of action.
Mapping incoming data sequence into a channel input sequence.
Inverse Mapping the channel output sequence into an output data sequence.
The final target is that the overall effect of the channel noise should be minimized.
The mapping is done by the transmitter, with the help of an encoder, whereas the inverse mapping is done by the decoder in the receiver.
Channel Coding
Let us consider a discrete memoryless channel (δ) with Entropy H (δ)
Ts indicates the symbols that δ gives per second
Channel capacity is indicated by C
Channel can be used for every Tc secs
Hence, the maximum capability of the channel is C/Tc
The data sent = $\frac{H(\delta)}{T_s}$
If $\frac{H(\delta)}{T_s} \leq \frac{C}{T_c}$ it means the transmission is good and can be reproduced with a small probability of error.
In this, $\frac{C}{T_c}$ is the critical rate of channel capacity.
If $\frac{H(\delta)}{T_s} = \frac{C}{T_c}$ then the system is said to be signaling at a critical rate.
Conversely, if $\frac{H(\delta)}{T_s} > \frac{C}{T_c}$, then the transmission is not possible.
Hence, the maximum rate of the transmission is equal to the critical rate of the channel capacity, for reliable error-free messages, which can take place, over a discrete memoryless channel. This is called as Channel coding theorem.
Digital Communication - Error Control Coding
Noise or Error is the main problem in the signal, which disturbs the reliability of the communication system. Error control coding is the coding procedure done to control the occurrences of errors. These techniques help in Error Detection and Error Correction.
There are many different error correcting codes depending upon the mathematical principles applied to them. But, historically, these codes have been classified into Linear block codes and Convolution codes.
Linear Block Codes
In the linear block codes, the parity bits and message bits have a linear combination, which means that the resultant code word is the linear combination of any two code words.
Let us consider some blocks of data, which contains k bits in each block. These bits are mapped with the blocks which has n bits in each block. Here n is greater than k. The transmitter adds redundant bits which are (n-k) bits. The ratio k/n is the code rate. It is denoted by r and the value of r is r < 1.
The (n-k) bits added here, are parity bits. Parity bits help in error detection and error correction, and also in locating the data. In the data being transmitted, the left most bits of the code word correspond to the message bits, and the right most bits of the code word correspond to the parity bits.
Systematic Code
Any linear block code can be a systematic code, until it is altered. Hence, an unaltered block code is called as a systematic code.
Following is the representation of the structure of code word, according to their allocation.
If the message is not altered, then it is called as systematic code. It means, the encryption of the data should not change the data.
Convolution Codes
So far, in the linear codes, we have discussed that systematic unaltered code is preferred. Here, the data of total n bits if transmitted, k bits are message bits and (n-k) bits are parity bits.
In the process of encoding, the parity bits are subtracted from the whole data and the message bits are encoded. Now, the parity bits are again added and the whole data is again encoded.
The following figure quotes an example for blocks of data and stream of data, used for transmission of information.

The whole process, stated above is tedious which has drawbacks. The allotment of buffer is a main problem here, when the system is busy.
This drawback is cleared in convolution codes. Where the whole stream of data is assigned symbols and then transmitted. As the data is a stream of bits, there is no need of buffer for storage.
Hamming Codes
The linearity property of the code word is that the sum of two code words is also a code word. Hamming codes are the type of linear error correcting codes, which can detect up to two bit errors or they can correct one bit errors without the detection of uncorrected errors.
While using the hamming codes, extra parity bits are used to identify a single bit error. To get from one-bit pattern to the other, few bits are to be changed in the data. Such number of bits can be termed as Hamming distance. If the parity has a distance of 2, one-bit flip can be detected. But this can't be corrected. Also, any two bit flips cannot be detected.
However, Hamming code is a better procedure than the previously discussed ones in error detection and correction.
BCH Codes
BCH codes are named after the inventors Bose, Chaudari and Hocquenghem. During the BCH code design, there is control on the number of symbols to be corrected and hence multiple bit correction is possible. BCH codes is a powerful technique in error correcting codes.
For any positive integers m ≥ 3 and t < 2m-1 there exists a BCH binary code. Following are the parameters of such code.
Block length n = 2m-1
Number of parity-check digits n - k ≤ mt
Minimum distance dmin ≥ 2t + 1
This code can be called as t-error-correcting BCH code.
Cyclic Codes
The cyclic property of code words is that any cyclic-shift of a code word is also a code word. Cyclic codes follow this cyclic property.
For a linear code C, if every code word i.e., C = (C1, C2, ...... Cn) from C has a cyclic right shift of components, it becomes a code word. This shift of right is equal to n-1 cyclic left shifts. Hence, it is invariant under any shift. So, the linear code C, as it is invariant under any shift, can be called as a Cyclic code.
Cyclic codes are used for error correction. They are mainly used to correct double errors and burst errors.
Hence, these are a few error correcting codes, which are to be detected at the receiver. These codes prevent the errors from getting introduced and disturb the communication. They also prevent the signal from getting tapped by unwanted receivers. There is a class of signaling techniques to achieve this, which are discussed in the next chapter.
Spread Spectrum Modulation
A collective class of signaling techniques are employed before transmitting a signal to provide a secure communication, known as the Spread Spectrum Modulation. The main advantage of spread spectrum communication technique is to prevent interference whether it is intentional or unintentional.
The signals modulated with these techniques are hard to interfere and cannot be jammed. An intruder with no official access is never allowed to crack them. Hence, these techniques are used for military purposes. These spread spectrum signals transmit at low power density and has a wide spread of signals.
Pseudo-Noise Sequence
A coded sequence of 1s and 0s with certain auto-correlation properties, called as Pseudo-Noise coding sequence is used in spread spectrum techniques. It is a maximum-length sequence, which is a type of cyclic code.
Narrow-band and Spread-spectrum Signals
Both the Narrow band and Spread spectrum signals can be understood easily by observing their frequency spectrum as shown in the following figures.
Narrow-band Signals
The Narrow-band signals have the signal strength concentrated as shown in the following frequency spectrum figure.
Following are some of its features −
- Band of signals occupy a narrow range of frequencies.
- Power density is high.
- Spread of energy is low and concentrated.
Though the features are good, these signals are prone to interference.
Spread Spectrum Signals
The spread spectrum signals have the signal strength distributed as shown in the following frequency spectrum figure.
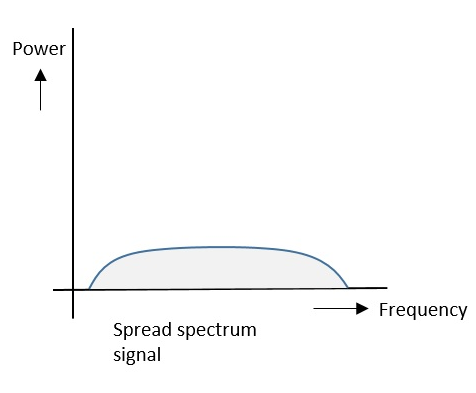
Following are some of its features −
- Band of signals occupy a wide range of frequencies.
- Power density is very low.
- Energy is wide spread.
With these features, the spread spectrum signals are highly resistant to interference or jamming. Since multiple users can share the same spread spectrum bandwidth without interfering with one another, these can be called as multiple access techniques.
FHSS and DSSS / CDMA
Spread spectrum multiple access techniques uses signals which have a transmission bandwidth of a magnitude greater than the minimum required RF bandwidth.
These are of two types.
- Frequency Hopped Spread Spectrum (FHSS)
- Direct Sequence Spread Spectrum (DSSS)
Frequency Hopped Spread Spectrum (FHSS)
This is frequency hopping technique, where the users are made to change the frequencies of usage, from one to another in a specified time interval, hence called as frequency hopping. For example, a frequency was allotted to sender 1 for a particular period of time. Now, after a while, sender 1 hops to the other frequency and sender 2 uses the first frequency, which was previously used by sender 1. This is called as frequency reuse.
The frequencies of the data are hopped from one to another in order to provide a secure transmission. The amount of time spent on each frequency hop is called as Dwell time.
Direct Sequence Spread Spectrum (DSSS)
Whenever a user wants to send data using this DSSS technique, each and every bit of the user data is multiplied by a secret code, called as chipping code. This chipping code is nothing but the spreading code which is multiplied with the original message and transmitted. The receiver uses the same code to retrieve the original message.
Comparison between FHSS and DSSS/CDMA
Both the spread spectrum techniques are popular for their characteristics. To have a clear understanding, let us take a look at their comparisons.
| FHSS | DSSS / CDMA |
|---|---|
| Multiple frequencies are used | Single frequency is used |
| Hard to find the users frequency at any instant of time | User frequency, once allotted is always the same |
| Frequency reuse is allowed | Frequency reuse is not allowed |
| Sender need not wait | Sender has to wait if the spectrum is busy |
| Power strength of the signal is high | Power strength of the signal is low |
| Stronger and penetrates through the obstacles | It is weaker compared to FHSS |
| It is never affected by interference | It can be affected by interference |
| It is cheaper | It is expensive |
| This is the commonly used technique | This technique is not frequently used |
Advantages of Spread Spectrum
Following are the advantages of spread spectrum −
- Cross-talk elimination
- Better output with data integrity
- Reduced effect of multipath fading
- Better security
- Reduction in noise
- Co-existence with other systems
- Longer operative distances
- Hard to detect
- Not easy to demodulate/decode
- Difficult to jam the signals
Although spread spectrum techniques were originally designed for military uses, they are now being used widely for commercial purpose.