
- Digital Communication - Home
- Analog to Digital
- Pulse Code Modulation
- Sampling
- Quantization
- Differential PCM
- Delta Modulation
- Techniques
- Line Codes
- Data Encoding Techniques
- Pulse Shaping
- Digital Modulation Techniques
- Amplitude Shift Keying
- Frequency Shift Keying
- Phase Shift Keying
- Quadrature Phase Shift Keying
- Differential Phase Shift Keying
- M-ary Encoding
- Information Theory
- Source Coding Theorem
- Channel Coding Theorem
- Error Control Coding
- Spread Spectrum Modulation
Digital Communication - Error Control Coding
Noise or Error is the main problem in the signal, which disturbs the reliability of the communication system. Error control coding is the coding procedure done to control the occurrences of errors. These techniques help in Error Detection and Error Correction.
There are many different error correcting codes depending upon the mathematical principles applied to them. But, historically, these codes have been classified into Linear block codes and Convolution codes.
Linear Block Codes
In the linear block codes, the parity bits and message bits have a linear combination, which means that the resultant code word is the linear combination of any two code words.
Let us consider some blocks of data, which contains k bits in each block. These bits are mapped with the blocks which has n bits in each block. Here n is greater than k. The transmitter adds redundant bits which are (n-k) bits. The ratio k/n is the code rate. It is denoted by r and the value of r is r < 1.
The (n-k) bits added here, are parity bits. Parity bits help in error detection and error correction, and also in locating the data. In the data being transmitted, the left most bits of the code word correspond to the message bits, and the right most bits of the code word correspond to the parity bits.
Systematic Code
Any linear block code can be a systematic code, until it is altered. Hence, an unaltered block code is called as a systematic code.
Following is the representation of the structure of code word, according to their allocation.
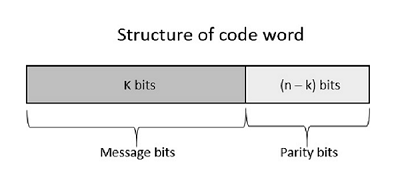
If the message is not altered, then it is called as systematic code. It means, the encryption of the data should not change the data.
Convolution Codes
So far, in the linear codes, we have discussed that systematic unaltered code is preferred. Here, the data of total n bits if transmitted, k bits are message bits and (n-k) bits are parity bits.
In the process of encoding, the parity bits are subtracted from the whole data and the message bits are encoded. Now, the parity bits are again added and the whole data is again encoded.
The following figure quotes an example for blocks of data and stream of data, used for transmission of information.

The whole process, stated above is tedious which has drawbacks. The allotment of buffer is a main problem here, when the system is busy.
This drawback is cleared in convolution codes. Where the whole stream of data is assigned symbols and then transmitted. As the data is a stream of bits, there is no need of buffer for storage.
Hamming Codes
The linearity property of the code word is that the sum of two code words is also a code word. Hamming codes are the type of linear error correcting codes, which can detect up to two bit errors or they can correct one bit errors without the detection of uncorrected errors.
While using the hamming codes, extra parity bits are used to identify a single bit error. To get from one-bit pattern to the other, few bits are to be changed in the data. Such number of bits can be termed as Hamming distance. If the parity has a distance of 2, one-bit flip can be detected. But this can't be corrected. Also, any two bit flips cannot be detected.
However, Hamming code is a better procedure than the previously discussed ones in error detection and correction.
BCH Codes
BCH codes are named after the inventors Bose, Chaudari and Hocquenghem. During the BCH code design, there is control on the number of symbols to be corrected and hence multiple bit correction is possible. BCH codes is a powerful technique in error correcting codes.
For any positive integers m ≥ 3 and t < 2m-1 there exists a BCH binary code. Following are the parameters of such code.
Block length n = 2m-1
Number of parity-check digits n - k ≤ mt
Minimum distance dmin ≥ 2t + 1
This code can be called as t-error-correcting BCH code.
Cyclic Codes
The cyclic property of code words is that any cyclic-shift of a code word is also a code word. Cyclic codes follow this cyclic property.
For a linear code C, if every code word i.e., C = (C1, C2, ...... Cn) from C has a cyclic right shift of components, it becomes a code word. This shift of right is equal to n-1 cyclic left shifts. Hence, it is invariant under any shift. So, the linear code C, as it is invariant under any shift, can be called as a Cyclic code.
Cyclic codes are used for error correction. They are mainly used to correct double errors and burst errors.
Hence, these are a few error correcting codes, which are to be detected at the receiver. These codes prevent the errors from getting introduced and disturb the communication. They also prevent the signal from getting tapped by unwanted receivers. There is a class of signaling techniques to achieve this, which are discussed in the next chapter.