Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
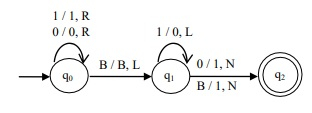
Design a TM that increments a binary number by 1
Turing’s machine is more powerful than both finite automata and pushdown automata. These machines are as powerful as any computer we have ever built.
Formal Definition of Turing Machine
A Turing machine can be formally described as seven tuples
(Q,X, Σ,δ,q0,B,F)
Where,
Q is a finite set of states.
X is the tape alphabet
Σ is the input alphabet
δ is a transition function: δ:QxX→QxXx{left shift, right shift}
q0 is the initial state
B is the blank symbol
F is the final state.
A Turing Machine (TM) is a mathematical model which consists of an infinite length tape divided into cells on which input is given. It consists of a head which reads the input tape. A state register stores the state of the Turing machine.
After reading an input symbol, it is replaced with another symbol, its internal state is changed, and it moves from one cell to the right or left. If the TM reaches the final state, the input string is accepted, otherwise the string is rejected.
The Turing machine has a read/write head. So, we can write on the tape.
Algorithm
Replace the trailing 1‟s to 0.
Replace the first „0‟ from the right end by 1.
Example
Binary increment means adding 1 to the given input.
Input - 0111
Output - 1000
Input - 10000
Output - 10001
The Turing Machine that increments a binary number by 1 is as follows −
2K+ Views
To Continue Learning Please Login