Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Design a Moore machine for some binary input sequence.
Problem
Design a Moore machine for a binary input sequence such that if it has a substring 101, the machine outputs A, if the input has substring 110, it outputs B otherwise it outputs C.
Solution
For designing such a machine, we will check two conditions, and those are 101 and 110. If we get 101, the output will be A, and if we recognize 110, the output will be B. For other strings, the output will be C.
Moore machine has 6 tuples
(Q, q0, Σ, O, δ, λ)
Where,
- Q: Finite set of states
- q0: Initial state of machine
- Σ: Finite set of input symbols
- O: Output alphabet
- δ: Transition function where Q × Σ → Q
- λ: Output function where Q → O
The partial diagram will be as follows −
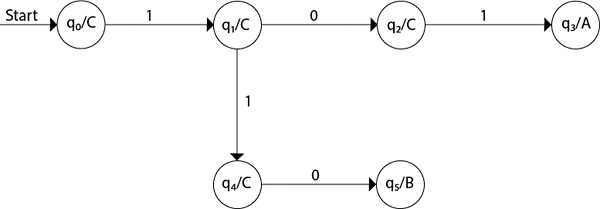
Example 1
Now, we will insert the possibilities of 0's and 1's for each state.
Thus, the Moore machine becomes as follows −
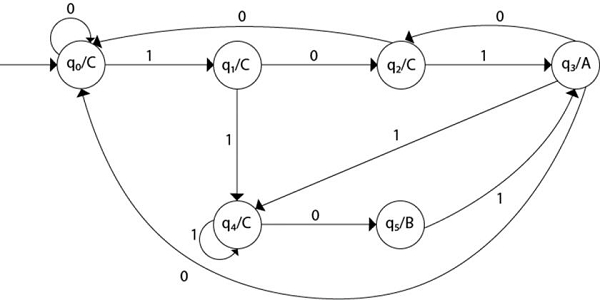
Explanation
- Step 1 − q0 is the start state on input ‘0’ goes to q0 and on ‘1’ goes to q1 generating output C.
- Step 2 − q1 on ‘0’ goes to q2 and on ‘1’ goes to q4 generating output C.
- Step 3 − q2 on ‘0’ goes to q0 and on ‘1’ goes to q3 generating output C.
- Step 4 − q3 on input ‘0’ goes to q2 and to q0 and on ‘1’ goes to q4 generating output A.
- Step 5 − q4 on input ‘0’ goes to q5 and on ‘1’ goes to q4 generating output C.
- Step 6 − q5 on input 1 goes to q3 generating an output B.
Example 2
Construct a Moore machine On input string bababbb, the output is 01100100.
Input alphabet − Σ = {a, b}
Output alphabet − Γ = {0, 1}
States − q0, q1, q2, q3
State Transition table
The transition table is as follows −
| Current State | a | b | Output |
|---|---|---|---|
| q0 | q3 | q2 | 0 |
| q1 | q1 | q0 | 0 |
| q2 | q2 | q3 | 1 |
| q3 | q0 | q1 | 0 |
State Transition diagram
The transition diagram is as follows −