Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Design a TM which recognizes palindromes over = {a, b}
Algorithm
Step 1 - If there is no input, reach the final state and halt.
Step 2 - If the input = “a‟, then traverse forward to process the last symbol = “a‟. Convert both a‟s to B‟.
Step 3 - Move left to read the next symbol.
Step 4 - If the input = “b‟, replace it by B and move right to process its equivalent “B‟ at the rightmost end.
Step 5 - Convert the last ’b’ to ‘B’.
Step 6 - Move left and process step 2 – 5 until there are no more inputs to process.
Step 7 - If the machine reaches the final state after processing the entire input string, then the string is a palindrome that halts the machine.
Turing Machine
The turing machine is as follows −
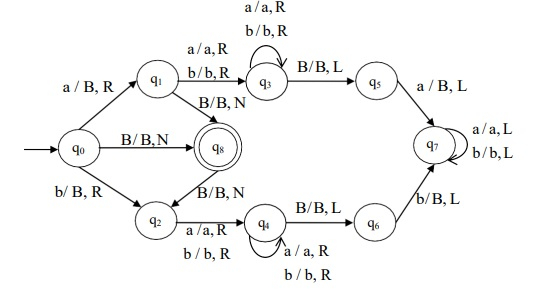
The Turing machine, M is given by M = (Q, Σ, Γ, δ, q0, B, F)
Where,
Q = {q0, q1, q2, q3, q4, q5, q6, q7, q8}
Σ = {a, b}
Γ = {a, b, B}
δ ⇒ Given by the above mentioned transition diagram,
q0 = {q0}
B = {B}
F = {q8}
Consider a string aabbaa, as shown below −
14K+ Views
