Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
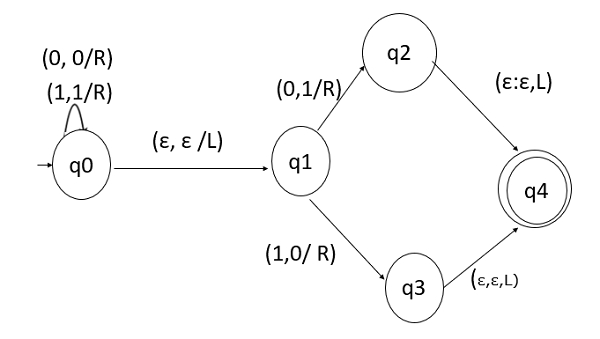
Construct a TM for a binary number as an input and replace the last digit with its Boolean complement?
Problem
Design a TM (Turing Machine) that takes a binary number as an input and replaces the last digit of the string with its Boolean complement.
Solution
A Turing machine is a 7-tuple (Q, ∑, Γ, δ, q0, qaccept , qreject)
Where,
Q is a finite set of states.
∑ is the input alphabet that does not contain the blank symbol t.
Γ is the tape alphabet, where t ∈ Γ and ∑ ⊆ Γ.
δ − (Q × Γ) → (Q × Γ × {L, R}) is the transition function.
q0 ∈ Q is the start state.
qaccept ∈ Q is the accept state.
qreject ∈ Q is the reject state, where qreject ≠qaccept.
In this TM,
In state q0, we will read all inputs until a blank symbol is encountered.
If a blank is found, we move one place LEFT.
Now, we have two options: either, the last digit is 0 or 1.
If it is 0, then replace it with 1, or vice versa.
State q4 is the final state.
The Turing Machine will be as follows if the binary number is taken as an input and if the last digit of the string is replaced with its Boolean complement.
211 Views
