Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct a TM for adding 1 to a binary natural number?
A Turing machine (TM) can be formally described as seven tuples −
(Q,X, ∑, δ,q0,B,F)
Where,
Q is a finite set of states.
X is the tape alphabet.
∑ is the input alphabet.
δ is a transition function: δ:QxX->QxXx{left shift, right shift}.
q0 is the initial state.
B is the blank symbol.
F is the final state.
Binary numbers
1 = 1
2 = 10
3 = 11
4 = 100
5 = 101
6 = 110
. . .
Algorithm
Step 1 − Move to the right end of the string.
Step 2 − Repeat:
If the current cell contains 1, write 0 and move left until the current cell contains 0 or blank.
Step 3 − Write a 1.
Step 4 − Move to the left end of the string and halt.
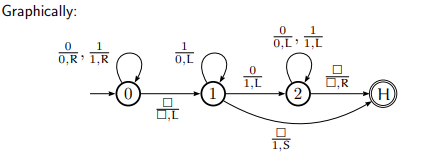
Let ❑ call it as B.
The TM instructions are as follows −
(0, 0, 0, R, 0) Scan right.
(0, 1, 1, R, 0) Scan right.
(0,B ,B , L, 1) Found right end of string.
(1, 1, 0, L, 1) Write 0 and move left with carry bit.
(1, 0, 1, L, 2) Write 1, adding done.
(1,B , 1, S, Halt) Write 1, done and in proper position
(2, 0, 0, L, 2) Scan left.
(2, 1, 1, L, 2) Scan left.
(2, B, B , R, Halt) Reached left end of string and halt.
Instantaneous description: 11 + 1 =2???
State 0 − B 1 1 B Scan right
State 0 − B 1 1 B
State 0 − B 1 1 B Finished scan.
State 1 − B 1 1 B 1 to 0
State 1 − B 1 0 B 1 to 0
State 1 − B 0 0 B 0 to 1
Halt − B 1 0 0 B Done!
447 Views
