
- Converting Fractions to Decimals
- Home
- Writing a Decimal and a Fraction for a Shaded Region
- Converting a Fraction With a Denominator of 10 or 100 to a Decimal
- Converting a Fraction With a Denominator of 100 or 1000 to a Decimal
- Converting a Proper Fraction With a Denominator of 2, 4, or 5 to a Decimal
- Converting a Mixed Number With a Denominator of 2, 4, or 5 to a Decimal
- Converting a Fraction to a Terminating Decimal - Basic
- Converting a Fraction to a Terminating Decimal - Advanced
- Converting a Fraction to a Repeating Decimal - Basic
- Converting a Fraction to a Repeating Decimal - Advanced
- Using a Calculator to Convert a Fraction to a Rounded Decimal
- Converting a Mixed Number to a Terminating Decimal - Basic
- Converting a Mixed Number to a Terminating Decimal - Advanced
- Ordering Fractions and Decimals
Using a Calculator to Convert a Fraction to a Rounded Decimal
Introduction
An electronic calculator displays fractions as decimal approximations rounded up to certain number (8, 12 or any other number) of places of decimals depending upon the company, type and model.
In this lesson, we learn how to use a calculator to convert a fraction to a rounded decimal.
Suppose we want the value of a fraction to be rounded to n places of decimal. We take the value with first n+1 digits after the decimal point from the calculator and round to n places i.e., we take one more digit than the required number of places of decimals. Then we round off the last digit. If the last digit is 5 or more, we add 1 to the preceding digit and if 4 or less we drop the last digit and write the first four digits as it is.
For example, suppose we want the value of a fraction to be rounded to four places of decimal. We take the value with first five digits after the decimal point from the calculator and round to four places i.e., we take one more digit than the required number of places of decimals. Then we round off the last digit. If the last digit is 5 or more, we add 1 to the preceding digit and if 4 or less we drop the last digit and write the first four digits as it is.
Example 1
Using a calculator convert $\frac{47}{85}$ into a decimal rounded to four places of decimal.
Solution
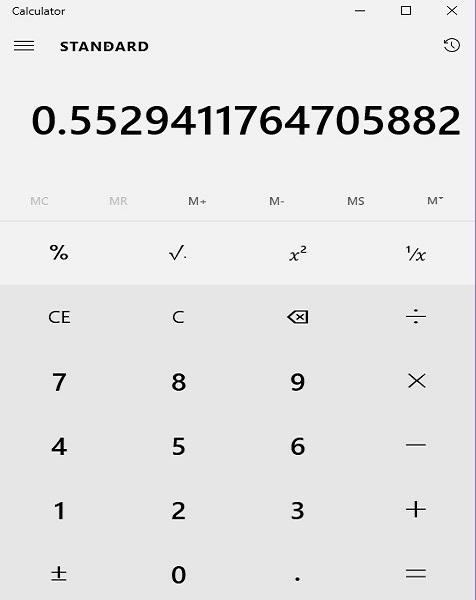
Step 1:
At first, we set up the fraction $\frac{47}{85}$ as a long division problem, dividing 47 by 85 using a calculator.
Step 2:
We find that on long division $\frac{47}{85} = 0.55294117...$
Step 3:
Since we must round to four places of decimal, we consider the first five (one more than four) digits after the decimal, i.e., 55294
Step 4:
The last digit is 4, so we drop it and keep the first four digits after the decimal only, i.e., 5529
Step 5:
So, $\frac{47}{85} = 0.5529$
Example 2
Using a calculator convert $\frac{67}{44}$ into a decimal rounded to four places of decimal.
Solution

Step 1:
At first, we set up the fraction as a long division problem, dividing 67 by 44
Step 2:
We find that on long division $\frac{67}{44} = 1.522727272...$
Step 3:
Since we must round to four places of decimal, we consider the first five (one more than four) digits after the decimal, i.e., 52272
Step 4:
The last digit is 2, so we drop it and keep the first four digits after the decimal only, i.e., 5227
Step 5:
So, $\frac{67}{44} = 1.5227$
Example 3
Using a calculator convert $\frac{86}{77}$ into a decimal rounded to four places of decimal.
Solution

Step 1:
At first, we set up the fraction as a long division problem, dividing 86 by 77
Step 2:
We find that on long division $\frac{86}{77} = 1.11688311...$
Step 3:
Since we must round to four places of decimal, we consider the first five (one more than four) digits after the decimal, i.e., 11688
Step 4:
The last digit is 8, so we add 1 to preceding digit which is also 8 to make it 9 and therefore rounding leads to, 1169
Step 5:
So, $\frac{86}{77} = 1.1169$