
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Convert the following LEX program into Lexical Analyzer.\\nAUXILIARY DEFINITIONS\\n −\\n −\\n −\\nTRANSLATION RULES\\n a{ }\\n abb{ }\\n a*b+
Solution
- Convert the pattern into NFA’s
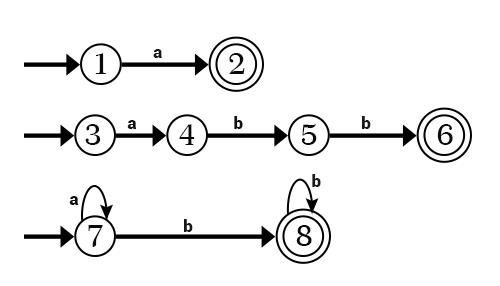
- Make a Combined NFA
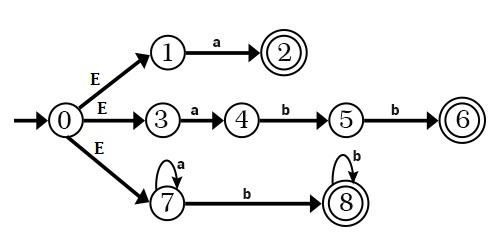
- Convert NFA to DFA
A = ε − closure (0) = {0, 1, 3, 7}
The transition on symbols a, b from state A
For State A

ε − closure (Ta) ε − closure (Tb)
= ε − closure ({2, 4, 7}) = ε − closure ({8})
= {2, 4, 7} = B = {8} = C
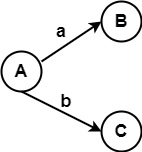
For State B
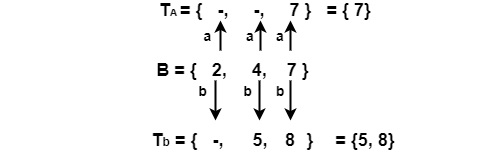
ε − closure (7) = {7} = D ε − closure ({5, 8}) = {5, 8} = E
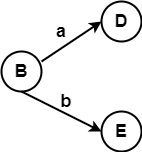
For State C
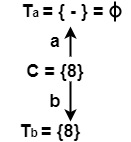
ε − closure (?) = ? | ε − closure (8) = {8} = C
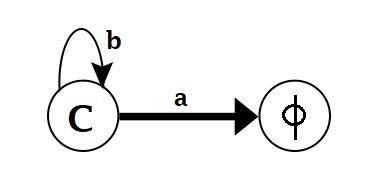
For State D
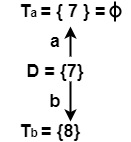
ε − closure (7) = {7} = D | ε − closure (8) = {8} = C
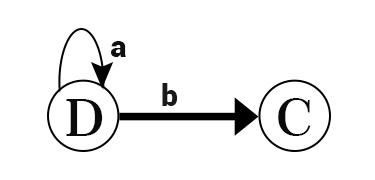
For State E
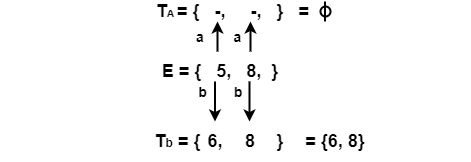
ε − closure (?) = ? | ε − closure {(6, 8)} = {6, 8} = F
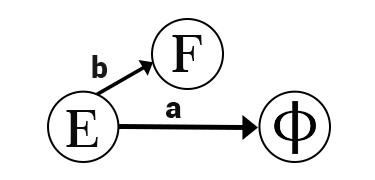
For State F
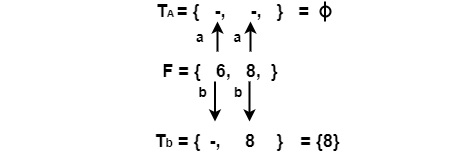
ε − closure (?) = ? | ε − closure (8) = {8} = C
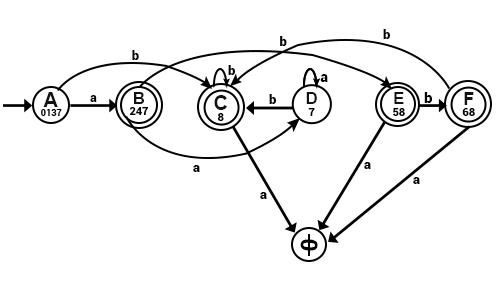
Combining all transition Diagrams, we get a complete DFA. Since states 2, 6, 8 are final states in NFA.
States in NFA having their states, i.e., 247, 8, 58, 68 are final states.
| State | A | b | Token Recognize |
|---|---|---|---|
| 0137 | 247 | 8 | none |
| 247 | 7 | 58 | a |
| 8 | ∅ | 8 | a*b+ |
| 7 | 7 | 8 | none |
| 58 | ∅ | 68 | a*b+ |
| 68 | ∅ | 8 | abb |
| ∅ | ∅ | ∅ | none |
Tokens Recognized
0137 → No state in {0, 1, 3, 7} is Final State. Therefore, no token will be recognized by this state.
247 → State 2 in this state is the final state. State 2 accepts a combined NFA. Therefore, 247 will accept a.
8 → 8 is the Final State in combined NFA. It accepts a*b+ in the combined NFA.
7 → 7 is not the final state & therefore it accepts nothing.
58 →8 is the final state, but 5 is a non-final state. State 8 accepts a∗b+in combined NFA. Therefore 58 will accept a*b+.
68 → Both states 6 & 8 are final states. But 6 accepts abb, and 8 accepts a*b+ in combined NFA. But abb comes before a*b+ in the Translation rules. Therefore state 68 will accept token abb.

