Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Hexadecimal Number System
Hexadecimal Number System is one the type of Number Representation techniques, in which there value of base is 16. That means there are only 16 symbols or possible digit values, there are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Where A, B, C, D, E and F are single bit representations of decimal value 10, 11, 12, 13, 14 and 15 respectively. It requires only 4 bits to represent value of any digit. Hexadecimal numbers are indicated by the addition of either an 0x prefix or an h suffix.
Position of every digit has a weight which is a power of 16. Each position in the Hexadecimal system is 16 times more significant than the previous position, that means numeric value of an hexadecimal number is determined by multiplying each digit of the number by the value of the position in which the digit appears and then adding the products. So, it is also a positional (or weighted) number system.
Representation of Hexadecimal Number
Each Hexadecimal number can be represented using only 4 bits, with each group of bits having a distich values between 0000 (for 0) and 1111 (for F = 15 = 8+4+2+1). The equivalent binary number of Hexadecimal number are as given below.
| Hex digit | 1 | 0 | 2 | 3 | 4 | 5 | 6 | 7 |
| Binary | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| Hex digit | 8 | 9 | A = 10 | B = 11 | C = 12 | D = 13 | E = 14 | F = 15 |
| Binary | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Hexadecimal number system is similar to Octal number system. Hexadecimal number system provides convenient way of converting large binary numbers into more compact and smaller groups.
| Most Significant Bit (MSB) | Hex Point | Least Significant Bit (LSB) | |||
|---|---|---|---|---|---|
| 162 | 161 | 160 | 16-1 | 16-2 | 16-3 |
| 256 | 16 | 1 | 1/16 | 1/256 | 1/4096 |
Since base value of Hexadecimal number system is 16, so there maximum value of digit is 15 and it can not be more than 15. In this number system, the successive positions to the left of the hexadecimal point having weights of 160, 161, 162, 163and so on. Similarly, the successive positions to the right of the hexadecimal point having weights of 16-1, 16-2, 16-3and so on. This is called base power of 16. The decimal value of any hexadecimal number can be determined using sum of product of each digit with its positional value.
Example-1 − The number 512 is interpreted as
512=2x162+0x161+0x160=200
Here, right most bit 0 is the least significant bit (LSB) and left most bit 2 is the most significant bit (MSB).
Example-2 − The number 2015.0625 is interpreted as
2015.0625=7x162+13x161+15x160+1x16-1=7DF.10
Here, right most bit 0 is the least significant bit (LSB) and left most bit 7 is the most significant bit (MSB).
Example-3 A a decimal number 21 to represent in Hexadecimal representation
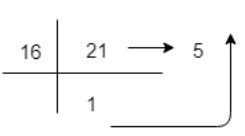
(21)10=1x161+5x160=(15)16 So, decimal value 21 is equivalent to 15 in Hexadecimal Number System.
Applications of Hexadecimal Number System
Hexadecimal Number System is commonly used in Computer programming and Microprocessors. It is also helpful to describe colors on web pages. Each of the three primary colors (i.e., red, green and blue) is represented by two hexadecimal digits to create 255 possible values, thus resulting in more than 16 million possible colors. Hexadecimal number system is used to describe locations in memory for every byte. These hexadecimal numbers are also easier to read and write than binary or decimal numbers for Computer Professionals.
Advantages and Disadvantages
The main advantage of using Hexadecimal numbers is that it uses less memory to store more numbers, for example it store 256 numbers in two digits whereas decimal number stores 100 numbers in two digits. This number system is also used to represent Computer memory addresses. It uses only 4 bits to represent any digit in binary and easy to convert from hexadecimal to binary and vice-versa. It is easier to handle input and output in the hexadecimal form. There is wide number of advantages in data science field, artificial intelligence and machine learning.
The major disadvantage of Hexadecimal number system is that it may not an easy to read and write for people, and also difficult to perform operations like multiplications, divisions using hexadecimal number system. Hexadecimal numbers is most difficult number system for dealing with Computer’s data.
15’s and 16’s Complement of Hexadecimal (Base-16) Number
Simply, 15’s complement of a hexadecimal number is the subtraction of it’s each digits from F(=15). For example, 15’s complement of hexadecimal number 2030 is FFFF - 2030 = DFCF.
16’s complement of hexadecimal number is 15’s complement of given number plus 1 to the least significant bit (LSB). For example 8’s complement of hexadecimal number 2020 is (FFFF - 2030) + 1 = DFDF + 1 = DFE0. Please note that maximum digit of hexadecimal number system is F(=15), so addition of F+1 will be 0 with carry 1.
12K+ Views
