Construct a Turing Machine for L = {a^n b^n | n>=1}

The Turing machine (TM) is more powerful than both finite automata (FA) and pushdown automata (PDA). They are as powerful as any computer we have ever built.

Formal Definition of Turing Machine

A Turing machine can be formally described as seven tuples

(Q,X, Σ, δ,q0,B,F)

Where,

• Q is a finite set of states

• X is the tape alphabet

• Σ is the input alphabet

• δ is a transition function: δ:QxX→QxXx{left shift, right shift}

• q0 is the initial state

• B is the blank symbol

• F is the final state.

A Turing Machine (TM) is a mathematical model which consists of an infinite length tape divided into cells on which input is given. It consists of a head which reads the input tape. A state register stores the state of the Turing machine.

After reading an input symbol, it is replaced with another symbol, its internal state is changed, and it moves from one cell to the right or left. If the TM reaches the final state, the input string is accepted, otherwise rejected.

The Turing machine has a read/write head. So we can write on the tape.

Now, let us construct a Turing machine which accepts equal number of a’s and b’s,

The language it is generated is L ={ aⁿbⁿ | n>=1}, the strings that are accepted by the given language is −

L= {ab, aabb, aaabbb, aaaabbbb,………}

Example

Consider n=3 so, a³b³ , the tape looks like −

B= blank

We need to convert every ‘a’ as X and every ‘b’ as Y. If the Turing machine contains an equal number of X and Y then it reaches the final state.

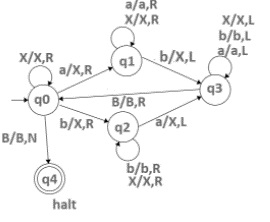
Step 1 − Consider the initial state as q0. This state replace ‘a’ as X and move to right, now state changes for q0 toq1, so the transition function is −

δ(q0, a) = (q1,X,R)

Step 2 − Move right until you see the blank symbol.

δ(q1, a) = (q1,a,R)
δ(q1, b) = (q1,b,R)

After reaching the blank symbol B, move left and change the state to q2, because we need to change the last ‘b’ to Y.

δ(q1, B) = (q2,B,L) //1st iteration
δ(q1, Y) = (q2,Y,L) // remaining iterations

Step 3 − When we see the symbol ‘b’, replace it as Y and change the state to q3 and move left.

δ(q2, B) = (q3,Y,L)

Step 4 − Move to left until reach the symbol X.

δ(q3, a) = (q3,a,L)
δ(q3, b) = (q3,b,L)

When we reach X move right and change the state as q0, and the next iteration is started.

After replacing every ‘a’ and ‘b’ as X and Y by changing the states to q0 to q4, we get the following −

δ(q0, Y) = (q4,Y,N)

N represents No movement.

q4 is the final state and q0 is the initial state of the Turing Machine, the intermediate states are q1, q2, q3.

Transition diagram

The transition diagram for Turing Machine is as follows −