Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Convert Sorted List to Binary Search Tree in C++
Suppose we have a singly linked list where elements are sorted in ascending order, we have to convert it to a height balanced BST. So if the list is like [-10, -3, 0, 5, 9], The possible tree will be like −
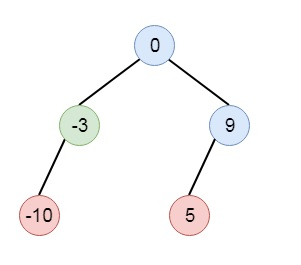
To solve this, we will follow these steps −
If the list is empty, then return null
Define a recursive method called sortedListToBST() this will take list start node
x := address of the previous node of mid node from list a
mid := exact mid node
create a new node with value by taking from the value of mid
nextStart := next of mid node
set mid next as null
right of node := sortedListToBST(nextStart)
if x is not null, then next of x = null and left of node := sortedListToBST(a)
return node
Example (C++)
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
class ListNode{
public:
int val;
ListNode *next;
ListNode(int data){
val = data;
next = NULL;
}
};
ListNode *make_list(vector<int> v){
ListNode *head = new ListNode(v[0]);
for(int i = 1; i<v.size(); i++){
ListNode *ptr = head;
while(ptr->next != NULL){
ptr = ptr->next;
}
ptr->next = new ListNode(v[i]);
}
return head;
}
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = right = NULL;
}
};
void inord(TreeNode *root){
if(root != NULL){
inord(root->left);
cout << root->val << " ";
inord(root->right);
}
}
class Solution {
public:
pair <ListNode*, ListNode*> getMid(ListNode* a){
ListNode* prev = NULL;
ListNode* fast = a;
ListNode* slow = a;
while(fast && fast->next){
fast = fast->next->next;
prev = slow;
slow = slow->next;
}
return {prev, slow};
}
TreeNode* sortedListToBST(ListNode* a) {
if(!a)return NULL;
pair<ListNode*, ListNode*> x = getMid(a);
ListNode* mid = x.second;
TreeNode* Node = new TreeNode(mid->val);
ListNode* nextStart = mid->next;
mid->next = NULL;
Node->right = sortedListToBST(nextStart);
if(x.first){
x.first->next = NULL;
Node->left = sortedListToBST(a);
}
return Node;
}
};
main(){
vector<int> v = {-10,-3,0,5,9};
ListNode *head = make_list(v);
Solution ob;
inord(ob.sortedListToBST(head));
}Input
[-10,-3,0,5,9]
Output
-10 -3 0 5 9
121 Views
