
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Binary Tree to Binary Search Tree Conversion in C++
To convert a binary tree to a binary search tree, use the inorder tree traversal of the tree. In inorder traversal, we first traverse the left subtree, then the root node, and then the right subtree. The nodes in inorder traversal of a binary search tree are in ascending order, so we find the inorder traversal of binary tree, sort it in ascending order, and place the sorted nodes in binary tree using inorder traversal to get the binary search tree.
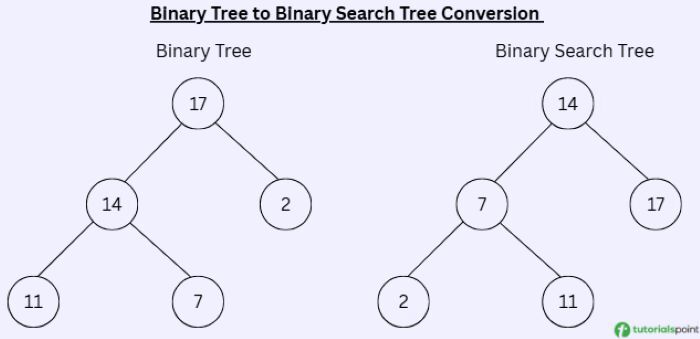
Understanding Binary Tree and Binary Search Tree
A binary tree is a special type of tree in which each node of the tree can have at most two child nodes (left and right). A binary search tree is a special type of binary tree that follows the conditions given below:
- The left child node's value is always less than the parent node.
- The right child node has a greater value than the parent node.
- All the nodes individually form a binary search tree.
Here are some example scenarios to convert the given binary tree to binary search tree:
Scenario 1
Input: Binary Tree Inorder Traversal: 11 -> 14 -> 7 -> 17 -> 2 Output: Binary Search Tree Inorder Traversal: 2 -> 7 -> 11 -> 14 -> 17
Scenario 2
Input: Binary Tree Inorder Traversal: 40 -> 20 -> 50 -> 10 -> 60 -> 30 -> 70 Output: Binary Search Tree Inorder Traversal: 10 -> 20 -> 30 -> 40 -> 50 -> 60 -> 70
Steps for Binary Tree to Binary Search Tree Conversion
Here are the steps to convert the given binary tree into a binary search tree while maintaining the original structure of the binary tree:
- Define an inorderTraversal() function to find and store the inorder traversal of the given binary tree into an array. It accepts the root node, an inorder array, and an index pointer.
- The countNodes() function counts the nodes in the binary tree and is used as the number of elements in the inorder array.
- In the inorderTraversal() function, first we recursively traverse the left subtree until we find a null value. After a null value is found, we return to its previous node and store it in the inorder array, increase the index by one, and traverse the right subtree.
- The above step is repeated until we have traversed the complete binary tree and stored its nodes in an array in inorder form.
- Sort the inorder array using the sort() function in ascending order to create a binary search tree. The nodes in inorder traversal of a binary search tree are in ascending order.
- In the arrayToBST() function, we traverse the binary tree in inorder and replace the nodes with sorted array elements. Then we print the inorder traversal of the binary search tree using the printInorder() function.
C++ Program for Binary Tree to Binary Search Tree Conversion
Here is the code implementation of the above-mentioned steps for binary tree to binary search tree conversion:
#include <iostream>
#include <algorithm>
using namespace std;
struct node
{
int data;
struct node *left;
struct node *right;
};
void inorderTraversal(struct node *node, int inorder[], int *index_ptr)
{
if (node == NULL)
return;
inorderTraversal(node->left, inorder, index_ptr);
inorder[*index_ptr] = node->data;
(*index_ptr)++;
inorderTraversal(node->right, inorder, index_ptr);
}
int countNodes(struct node *root)
{
if (root == NULL)
return 0;
return countNodes(root->left) +
countNodes(root->right) + 1;
}
void arrayToBST(int *arr, struct node *root, int *index_ptr)
{
if (root == NULL)
return;
arrayToBST(arr, root->left, index_ptr);
root->data = arr[*index_ptr];
(*index_ptr)++;
arrayToBST(arr, root->right, index_ptr);
}
struct node *newNode(int data)
{
struct node *temp = new struct node;
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return temp;
}
void printInorder(struct node *node)
{
if (node == NULL)
return;
printInorder(node->left);
cout << node->data << " ";
printInorder(node->right);
}
int main()
{
struct node *root = NULL;
root = newNode(17);
root->left = newNode(14);
root->right = newNode(2);
root->left->left = newNode(11);
root->left->right = newNode(7);
cout << "Inorder Traversal of the binary Tree: " << endl;
printInorder(root);
int n = countNodes(root);
int *arr = new int[n];
int i = 0;
inorderTraversal(root, arr, &i);
std::sort(arr, arr + n);
i = 0;
arrayToBST(arr, root, &i);
delete[] arr;
cout << endl
<< "Inorder Traversal of the converted BST: " << endl;
printInorder(root);
return 0;
}
The output of the above code is as follows:
Inorder Traversal of the binary Tree: 11 14 7 17 2 Inorder Traversal of the converted BST: 2 7 11 14 17
The time and space complexity of the above code is O(n log n) and O(n), respectively.

