
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Balance a Binary Search Tree in c++
In this article, we have a binary search tree and our task is to balance the given binary search tree. A binary search tree is a tree data structure and a special type of binary tree that follows the conditions given below:
- The left child node's value is always less than the parent node.
- The right child node has a greater value than the parent node.
- All the nodes individually form a binary search tree.
- The inorder traversal of nodes in BST are in ascending order.
In a balanced binary search tree, the maximum difference of depth between right and left subtree is of 1. Here is a visual example of unbalanced and balance BST:
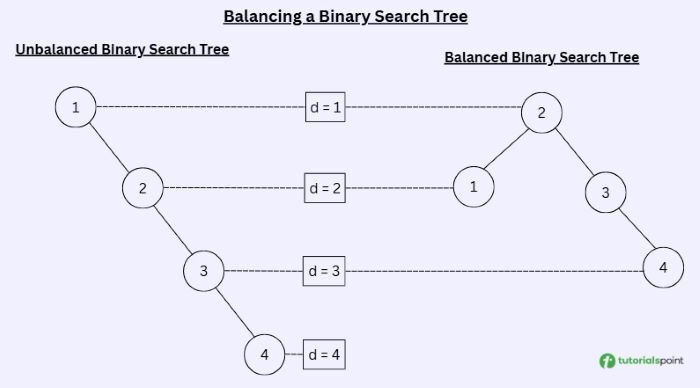
In the above figure, we can see in the unbalanced BST that the difference between right and left subtree is of 4. While, in the balanced subtree, the difference of depths of right and left subtree is 1.
Steps to Balance a Binary Search Tree
Following are the steps to balance a given unbalanced binary search tree:
- Create an array with inorder traversal of the given binary search tree.
- Since the inorder array will be a sorted array, divide the array in two subarray around middle element.
- The middle element becomes root node, left and right subarray becomes left and right subtree respectively.
- Repeat the above two steps until complete inorder array is traversed.
- Print the unbalanced and balanced binary search tree using printLevel() function.
C++ Program to Balance a Binary Search Tree
Here is an example code of the above-mentioned steps for balancing an unbalanced binary search tree:
#include <bits/stdc++.h>
using namespace std;
struct TreeNode {
int val;
TreeNode *left, *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
// Global vector to store inorder traversal
vector<int> arr;
// For inorder travesal
void inorder(TreeNode* node) {
if (!node)
return;
inorder(node->left);
arr.push_back(node->val);
inorder(node->right);
}
// Constructing balanced BST from sorted inorder array
TreeNode* construct(int low, int high) {
if (low > high)
return NULL;
int mid = low + (high - low) / 2; // root as middle element
TreeNode* root = new TreeNode(arr[mid]);
root->left = construct(low, mid - 1); // Recursively construct left subtree
root->right = construct(mid + 1, high); // Recursively construct right subtree
return root;
}
TreeNode* balanceBST(TreeNode* root) {
arr.clear();
inorder(root);
return construct(0, arr.size() - 1);
}
void printLevel(TreeNode* root) {
if (!root)
return;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
int size = q.size();
bool hasNonNull = false;
queue<TreeNode*> temp = q;
while (!temp.empty()) {
if (temp.front() != nullptr) {
hasNonNull = true;
break;
}
temp.pop();
}
if (!hasNonNull)
break;
for (int i = 0; i < size; i++) {
TreeNode* node = q.front();
q.pop();
if (node) {
cout << node->val << " ";
q.push(node->left);
q.push(node->right);
} else {
cout << "\ ";
q.push(nullptr);
q.push(nullptr);
}
}
cout << "\n";
}
}
int main() {
TreeNode* root = new TreeNode(1);
root->right = new TreeNode(2);
root->right->right = new TreeNode(3);
root->right->right->right = new TreeNode(4);
cout << "Given BST:\n";
printLevel(root);
TreeNode* balanced = balanceBST(root);
cout << "\nBalanced BST:\n";
printLevel(balanced);
return 0;
}
The output of the above code is as follows:
Given BST: 1 \ 2 \ \ \ 3 \ \ \ \ \ \ \ 4 Balanced BST: 2 1 3 \ \ \ 4
The time and space complexity of the above code is O(n) and O(n), respectively.

