Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Binary Search Tree - Delete Operation in C++
Binary search tree (BST) is a special type of tree which follows the following rules −
left child node’s value is always less than the parent Note
right child node has a greater value than the parent node.
all the nodes individually form a binary search tree.
Example of a binary search tree (BST) −
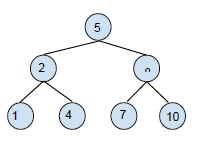
A binary search tree is created in order to reduce the complexity of operations like search, find minimum and maximum.
Delete Operation binary search tree (BST)
delete operation is dropping the specified node from the tree. in case deleting the nodes, there are three possibilities −
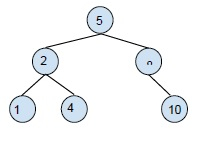
Deleting a leaf node from the tree: The simplest deletion is the deletion of a leaf node from the binary search tree. For deleting the leaf node only the leaf gets affected. Example,
deleting the leaf node 7 gives,
Deleting the node with one child node: for this deletion, you need to replace the child node with the node to be deleted and then delete it. Example,
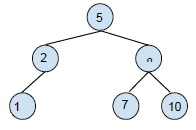
Deleting 2 from the BST
Deleting the node with two child nodes: Here the node to be deleted has two child nodes. So, we will use in the order form of the tree, here we will delete the element and select its inorder neighbor for its place and recreate the rest. Example,
Deleting 5 from the BST will return the following tree.
Example
#include<stdio.h>
#include<stdlib.h>
struct node{
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void inordertraversal(struct node *root){
if (root != NULL){
inordertraversal(root->left);
printf("%d ", root->key);
inordertraversal(root->right);
}
}
struct node* insert(struct node* node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
struct node * minValueNode(struct node* node){
struct node* current = node;
while (current && current->left != NULL)
current = current->left;
return current;
}
struct node* deleteNode(struct node* root, int key){
if (root == NULL) return root;
if (key < root->key)
root->left = deleteNode(root->left, key);
else if (key > root->key)
root->right = deleteNode(root->right, key);
else{
if (root->left == NULL){
struct node *temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL){
struct node *temp = root->left;
free(root);
return temp;
}
struct node* temp = minValueNode(root->right);
root->key = temp->key;
root->right = deleteNode(root->right, temp->key);
}
return root;
}
int main(){
struct node *root = NULL;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
printf("Inorder traversal of the given tree \n");
inordertraversal(root);
printf("\nDelete 20\n");
root = deleteNode(root, 20);
printf("Inorder traversal of the modified tree \n");
inordertraversal(root);
printf("\nDelete 30\n");
root = deleteNode(root, 30);
printf("Inorder traversal of the modified tree \n");
inordertraversal(root);
printf("\nDelete 50\n");
root = deleteNode(root, 50);
printf("Inorder traversal of the modified tree \n");
inordertraversal(root);
return 0;
}Output
Inorder traversal of the given tree 20 30 40 50 60 70 80 Delete 20 Inorder traversal of the modified tree 30 40 50 60 70 80 Delete 30 Inorder traversal of the modified tree 40 50 60 70 80 Delete 50 Inorder traversal of the modified tree 40 60 70 80
4K+ Views
