Binary Search Tree to Greater Sum Tree in C++

In this article, we are given a binary search tree. Our task is to transform the given BST to a Greater Sum tree. A Greater Sum Tree with respect to the given BST is a tree where each node's value is replaced by the sum of all values greater than that node's value in the original BST.

Below is an example scenarios to convert the given BST to a Greater Sum Tree:

Example Scenario

Input: BST inorder traversal= {0, 1, 2, 3, 4, 5, 6, 7, 8}
Output: Greater Sum Tree = {36, 35, 33, 30, 26, 21, 15, 8, 0}
Explanation:
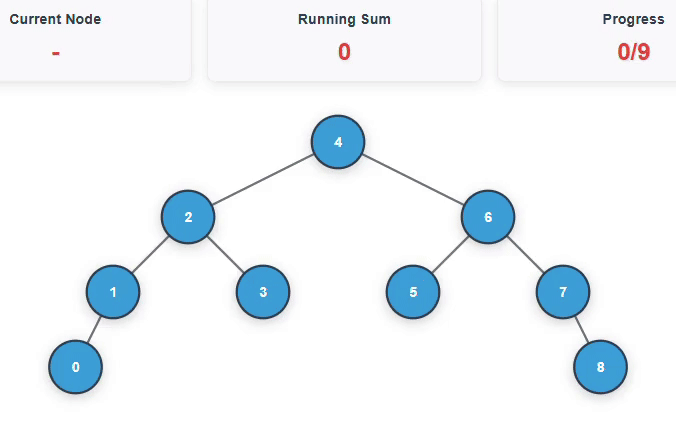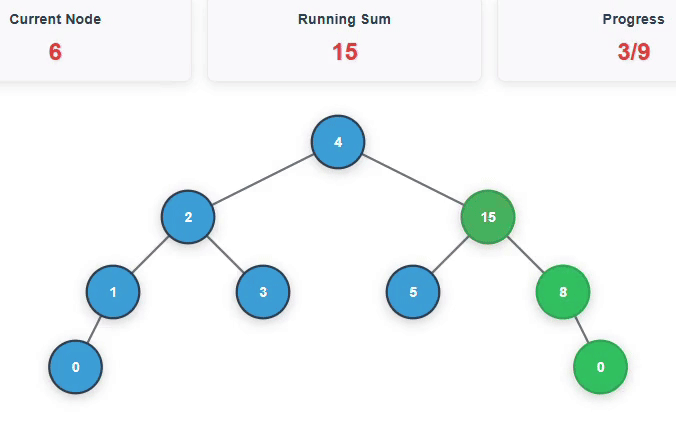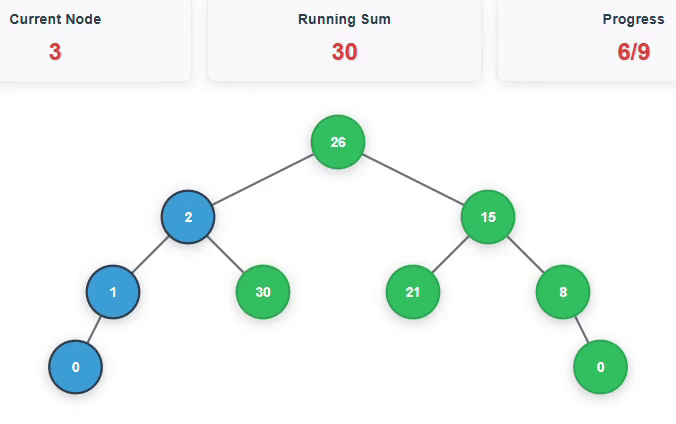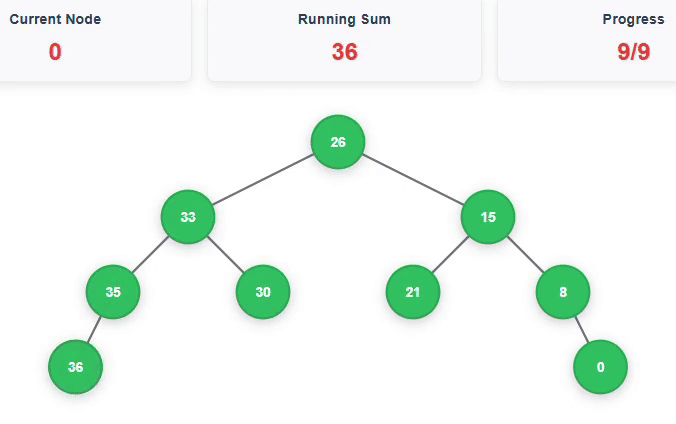
Reverse in-order traversal of BST: 8 -> 7 -> 6 -> 5 -> 4 -> 3 -> 2 -> 1 -> 0
Nodes > 8: None => Sum = 0, Nodes > 7: 8 => Sum = 8
Nodes > 6: 7, 8 => Sum = 15, Nodes > 5: 6, 7, 8 => Sum = 21
Nodes > 4: 5, 6, 7, 8 => Sum = 26, Nodes > 3: 4, 5, 6, 7, 8 => Sum = 30
Nodes > 2: 3, 4, 5, 6, 7, 8 => Sum = 33, Nodes > 1: 2, 3, 4, 5, 6, 7, 8 => Sum = 35
Nodes > 0: 1, 2, 3, 4, 5, 6, 7, 8 => Sum = 36
=> The Greater Sum Tree is {36, 35, 33, 30, 26, 21, 15, 8, 0}

Below is an animation to explain the above example:

Steps to Transform BST to Greater Sum Tree

Here are the steps to convert BST to Greater Sum Tree (GST):

• Initialize a runningSum variable to 0. It keeps a track of cumulative sum of all nodes with values greater than the current node.
• Traverse the given BST in a reverse in-order traversal, i.e., first traverse the right subtree, then the root, and then the Left subtree. You will get the nodes in descending order.
• At each node, store the original value of the current node, update the current node's value to the current runningSum, and add the original value originalVal to the runningSum for cumulative sum for the next node.
• Return the greater sum tree when all the nodes have been visited and converted.

Binary Search Tree to Greater Sum Tree Conversion in C++

Following is the C++ program to implement the above-mentioned steps for transforming the given BST to a greater sum tree. Here -1 represents null nodes:

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

struct TreeNode
{
    int val;
    TreeNode *left;
    TreeNode *right;

    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

TreeNode *buildTree(vector<int> &arr)
{
    if (arr.empty() || arr[0] == -1)
        return NULL;

    TreeNode *root = new TreeNode(arr[0]);
    queue<TreeNode *> q;
    q.push(root);
    int i = 1;

    while (!q.empty() && i < arr.size())
    {
        TreeNode *curr = q.front();
        q.pop();

        // Left child
        if (i < arr.size())
        {
            if (arr[i] != -1)
            {
                curr->left = new TreeNode(arr[i]);
                q.push(curr->left);
            }
            i++;
        }

        // Right child
        if (i < arr.size())
        {
            if (arr[i] != -1)
            {
                curr->right = new TreeNode(arr[i]);
                q.push(curr->right);
            }
            i++;
        }
    }
    return root;
}

// In-order traversal to display tree
void inorderPrint(TreeNode *root)
{
    if (!root)
        return;
    inorderPrint(root->left);
    cout << root->val << " ";
    inorderPrint(root->right);
}

int runningSum = 0;

TreeNode *bstToGst(TreeNode *root)
{
    if (!root)
        return NULL;

    // Traverse right subtree first
    bstToGst(root->right);

    // Updating current node
    int originalVal = root->val;
    root->val = runningSum;
    runningSum += originalVal;

    // Traverse left subtree
    bstToGst(root->left);

    return root;
}

int main()
{
    vector<int> v = {4, 1, 6, 0, 2, 5, 7, -1, -1, -1, 3, -1, -1, -1, 8};
    TreeNode *root = buildTree(v);

    cout << "Original BST: ";
    inorderPrint(root);
    cout << endl;

    root = bstToGst(root);

    cout << "Greater Sum Tree: ";
    inorderPrint(root);
    cout << endl;

    return 0;
}

The output of the above code is as follows:

Original BST: 0 1 2 3 4 5 6 7 8 
Greater Sum Tree: 36 35 33 30 26 21 15 8 0

The time and space complexity of the above code is O(n) and O(n), respectively.