Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
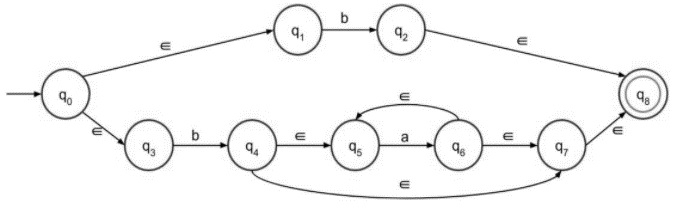
Construct ∈-NFA of Regular Language L = b + ba*
The ε transitions in Non-deterministic finite automata (NFA) are used to move from one state to another without having any symbol from the input set Σ.
ε-NFA is defined in 5 tuples representation
{Q, q0, Σ, δ, F}Where,
δ − Q × (Σ∪ε)→2Q
Q − Finite set of states
∑ − Finite set of the input symbol
q0 − Initial state
F − Final state
δ − Transition function
NFA without ε transition
NFA is defined in 5 tuples representation
{Q, q0, Σ, δ, F}Where,
δ − Q X Σ→ 2Q
Q − Finite set of states
∑ − Finite set of the input symbol
q0 − Initial state
F − Final state
δ − Transition function
NFA and NFA with epsilon both are almost the same; the only difference is their transition function.
Let’s consider the given language L = b+ba*
Steps for construction of ε-NFA
Step 1 − NFA with epsilon for a+ is given below −
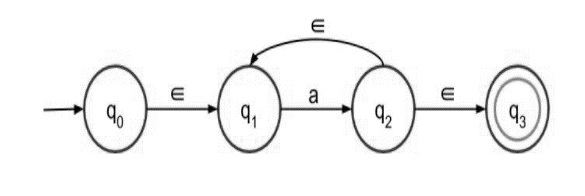
Here a+ means there must be at least one ‘a’ in the expression which is preceded by epsilon and succeeded by epsilon. It is nothing but there can be more than one ‘a’ in the expression.
Step 2 − NFA with epsilon for a* is given below −
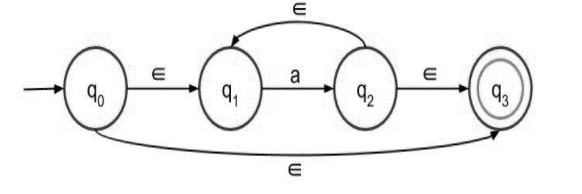
a* means there can be any number of ‘a’ in the expression, even 0 ( if the input symbol is null then also it is valid).
Step 3 − NFA with epsilon for (a+b) is given below −
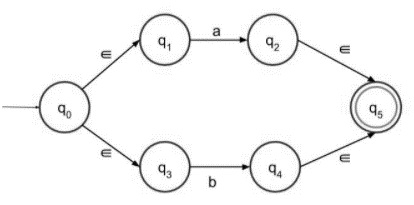
It accepts either a or b as an input, and both go to the final state.
Step 4 − NFA with epsilon for ab is given below −
Concatenating a and b with epsilon, and a must followed by b then only it can reach the final state.
Step 5 − The final NFA with epsilon for the given language is as follows −
L =b + ba* is divided into two parts.
The first part is simply ‘b’ which is easy to construct. Since both the terms are connected by using ‘+’ sign, there will be two paths coming out of the first node. The second part is to be drawn with the help of second step of construction, a* which is simply preceded by b.
4K+ Views
