Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
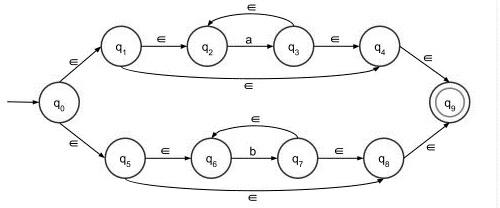
Construct a ∈-NFA for the language L = (a* + b*)
The ε transitions in Non-deterministic finite automata (NFA) are used to move from one state to another without having any symbol from input set Σ
ε-NFA is defined in five-tuple representation
{Q, q0, Σ, δ, F}Where,
δ − Q × (Σ∪ε)→2Q
Q − Finite set of states
Σ − Finite set of the input symbol
q0 − Initial state
F − Final state
δ − Transition function
NFA without ε transition
NFA is defined in five tuple representation
{Q, q0, Σ, δ, F}Where,
δ − Q X Σ→ 2Q
Q − Finite set of states
Σ − Finite set of the input symbol
q0 − Initial state
F − Final state
δ − Transition function
NFA and NFA with epsilon both are almost the same; the only difference is their transition function.
Let’s consider the given language L = (a*+b*)
Steps for construction ε-NFA
Step 1 − NFA with epsilon for a* is as follows −
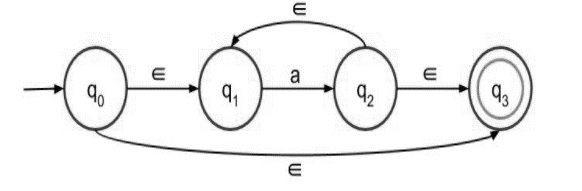
a* means there can be any number of ‘a’ in the expression, even 0 ( if the input symbol is null then also it is valid).
Step 2 − NFA with epsilon for b* is as follows −
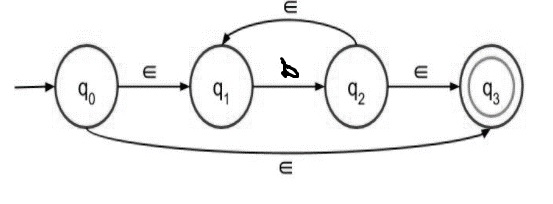
b* means there can be any number of b’s in the expression, even 0 (if input symbol is null then also it is valid).
Step 3 − Now construct a*+b* using first and second steps.
The given language is divided into two parts like a* and b* and add two steps by using ‘+’ sign to get the result.
3K+ Views
