
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is an acceptance of language by NFA with Epsilon?
The language L accepted by Non-deterministic finite automata (NFA) with ε, denoted by M= (Q, Σ, ?, q0, F) and can be defined as follows −
Let M= (Q, Σ, ?, q0, F) be a NFA with ε
Where,
- Q is a set of states
- Σ is input set
- δ is a transition function from Q x { Σ U ε } to 2Q
- q0 is start state
- F is a final state
The string w in L accepted by NFA can be represented as follows −
L(M)={w| w ∈ Σ* and ? transition for w from q0 reaches to F}
Example
Construct NFA with epsilon which accepts a language consisting the strings of any number of a’s followed by any number of b’s followed by any number of c’s
Solution
Here, any number of a’s or b’s or c’s means that there can be zero or more a’s followed by zero, more number of b’s followed by zero or more c’s.
Hence NFA with epsilon can be as follows −
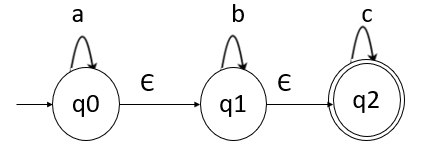
Normally, epsilon is not shown in the input string.
The NFA with epsilon is as follows −
M = ({q0,q1,q2},{a,b}, ?, q0,q2})
Explanation
- Step 1 − q0 is the initial state q0 on ‘a’ goes to q0 itself, and on epsilon transition q0 goes to q1.
- Step 2 − q1 on ‘b’ goes to q1 itself and on epsilon transition it goes to q2.
- Step 3 − q2 on ‘c’ goes to q2 itself which is the final state.
The transition table is as follows −
| State\ input symbol | a | b | C | ε |
|---|---|---|---|---|
| q0 | q0 | - | - | q1 |
| q1 | - | q1 | - | q2 |
| q2 | - | - | q2 | - |
Consider the string aabbcc as given below −
δ(q0,aabbcc) |- δ(q0,abbcc)
|- δ(q0,bbcc)
|- δ(q0, εbbcc)
|- δ(q1,bbcc)
|- δ(q1,bcc)
|- δ(q1,cc)
|- δ(q1, εcc)
|- δ(q2,cc)
|- δ(q2,c)
|- δ(q2, ε)
Thus, we reach the accept state, after scanning the compute input string.

