Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
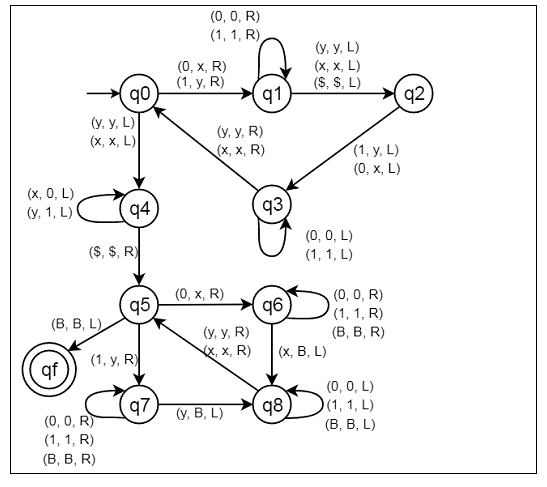
Construct a Turing Machine for language L = {ww | w ∈ {0,1}}
Here we will see how to make a Turing machine for language L = {WW |W belongs to {0, 1}}. So this represents a kind of language where we will use only two characters 0s and 1s. The w is a string. So if w = 10110, so the Turing machine will accept the string z = 1011010110.
To solve this, we will use this approach. The first thing is to find the midpoint of the string, we will convert a 0 to x and 1 to y. After continuously doing it a point is reached when all 0’s and 1’s has been converted into x and x respectively. Now, we are on the midpoint of the string. So, our first objective is completed.
Now, convert all x's and y's on the left of the midpoint into 0's and 1's. Now the first half the string is in the form of 0 and 1. The second half of the string is in the form of x and y.
Now, again start from the beginning of the string. If you have a 0 then convert it into x and move right till reaching the second half, here if we find x then convert it into a blank(B). Then traverse back till find an x or a x. We convert the 0 or 1 at the right of it into x or y respectively and correspondingly, convert its x or y in the second half of string into a blank(B).
Keep doing this till converted all symbols on the left part of the string into x and y and all symbols on the right of string into blanks. When one part is completely converted but still some symbols in the other half are left unchanged then the string will not be accepted. If we did not find an x or y in the second half for a corresponding 0 or 1 respectively in the first half. Then also string will not be accepted.
State Transition Diagram
3K+ Views
