Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct a PDA for language L = {0n 1m2m3n | n>=1, m>=1}
A push down automata (PDA) can be formally described as seven tuples
(Q, Σ,S, δ,q0,I,F)
Where,
- Q is finite number of states
- Σ is input alphabet
- S is stack symbol
- Δ is the transition function: QX(Σ∪{e})XSXQ
- q0 is the initial state (q0 belongs to Q)
- I is the initial state top symbol
- F is a set of accepting states(F belongs to Q)
Problem
Construct PDA for 0n1m2m3n where n,m≥1.
Solution
So, the strings which are generated by the given language are −
L={0123,011223,001233….}
The number of 1’s and 3’s are same and number of 2’s and 1’s are same
Construction of PDA for given problem
The PDA is as follows −
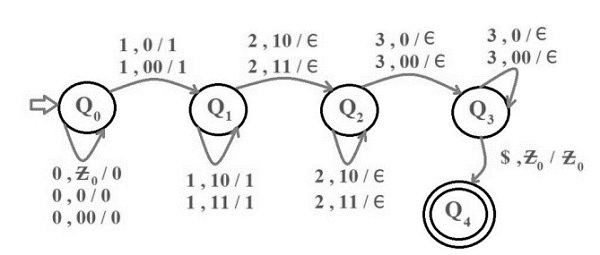
Explanation
Step 1 − First 0’s are pushed onto the stack.
Step 2 − Next 1’s are pushed into the stack.
Step 3 − For every 2 as input a 1 is popped out of stack.
Step 4 − If some 2’s are still left and top of stack is a 0 then string is not accepted by the PDA.
Step 5 − If 2’s are finished and top of stack is a 0 then for every 3 as input equal number of 0’s are popped out of stack.
Step 6 − If the string is finished and the stack is empty then the string is accepted by the PDA. Otherwise, the string is not accepted.
4K+ Views
