Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
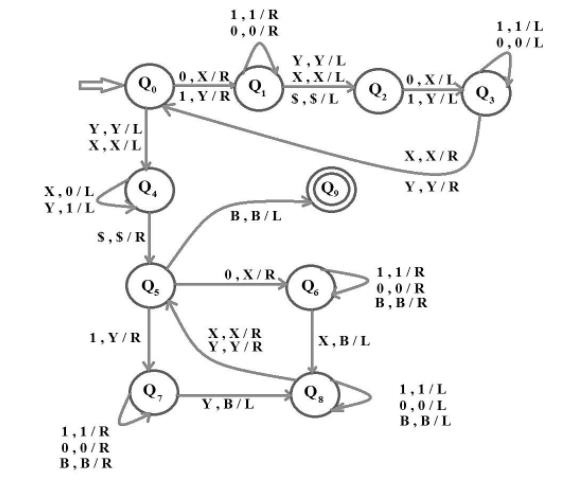
Construct a TM for the language L= {ww : w ∈ {0,1}}
Problem
The language L = {ww | w ε {0, 1}} having the string of 0’s and 1’s which is followed by itself
L={00,11,1100,0011,…..}
Solution
The logic for solving the problem is as follows −
- Find the midpoint of the string.
- Then match the symbols.
Explanation
Step 1 − First, we need to find the midpoint of the string.
Step 2 − We will make the first 0 to X or 1 to Y and then move R/W head to the right until the last character is found.
Step 3 − Then make this 0 to X or 1 to Y.
Step 4 − Now, we will move to the left and stop just before the first character which we make as X or Y at the beginning
Step 5 − Make the second character as X or Y depending on the value and similarly, we move to the right for the same.
Step 6 − After doing this continuously, all the 0s will be X and all the 1s will be Y and the R/W head will be at the middle of the string.
Step 7 − Now we will move the R//W head to the left of the string and convert X to 0 and Y to 1 continuously until we reach the beginning of the string.
Step 8 − After this is done, half of the string will be having 0s and 1s and the other half will be having Xs and Ys.
Step 9 − Now that the R/W head is on the first character, we will convert it to X if 0 or we will make it Y if it is 1 (as done earlier).
Step 10 − After the first character is converted, move the read-write head all the way to the right until we encounter the first X or Y (the second half of the string) and make it blank.
Step 11 − Then move all the way back to the character next to X or Y and then repeat the same.
Step 12 − After continuously doing the above step, if only Xs and Ys are left (only the first half portion is left, the second half will be blank) then the string will be accepted. Otherwise, it will be rejected.
The implementation of the same using the Turing machine (TM) is shown below−
Here, we have made the same using ten states where Q0 is the initial state and Q9 is the final.
The Turing Machine is as follows −
759 Views
