Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
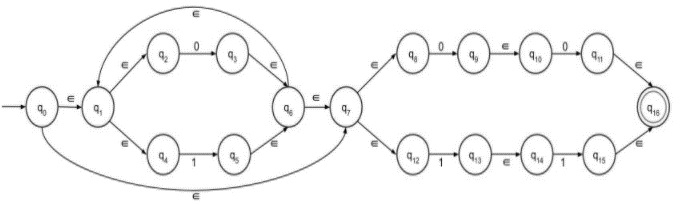
Construct ∈-NFA of Regular Language L = (0+1)*(00+ 11)
The ε transitions in Non-deterministic finite automata (NFA) are used to move from one state to another without having any symbol from input set Σ
ε-NFA is defined in five tuple
{Q, q0, Σ, δ, F}Where,
δ − Q × (Σ∪ε)→2Q
Q − Finite set of states
Σ − Finite set of the input symbol
q0 − Initial state
F − Final state
δ − Transition function
NFA without ε transition
NFA is defined in 5 tuple representation
{Q, q0, Σ, δ, F}Where,
δ − Q X Σ→ 2Q
Q − Finite set of states
Σ, − Finite set of the input symbol
q0 − Initial state
F − Final state
δ − Transition function
NFA and NFA with epsilon both are almost the same; the only difference is their transition function.
Let’s consider the given language L = 0(0+1)*1
Rules for construction of ε-NFA are as follows −
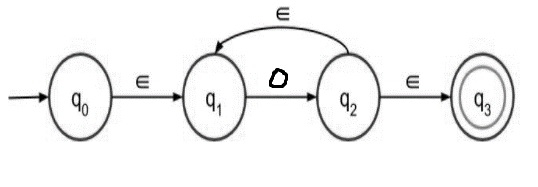
Step 1 − NFA with epsilon for 0+ is given below −
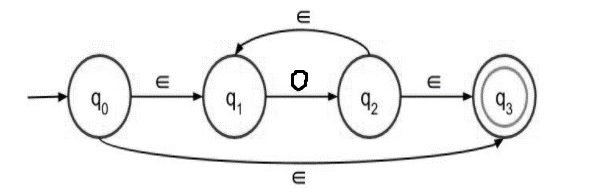
Step 2 − NFA with epsilon for 0* is given below −
Step 3 − NFA with epsilon for (0+1) is given below −
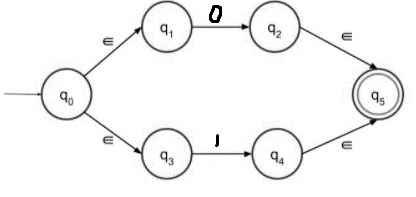
The above transition diagram accepts either 0 or 1 as input. Those two paths lead to the final state.
Step 4 − NFA with epsilon for 01 is given below −
For concatenation 0 must be followed by 1.
Step 5 −
ε-NFA for L = (0+1)*(00 + 11)
L = (0+1)*(00 + 11) is divided into two parts: (0+1)* and (00+11).
First construct the first part and then second part finally concatenate two parts to get the result.
First part − (0+1)*
With the help of step 3 we can easily construct (0+1)* as shown below −
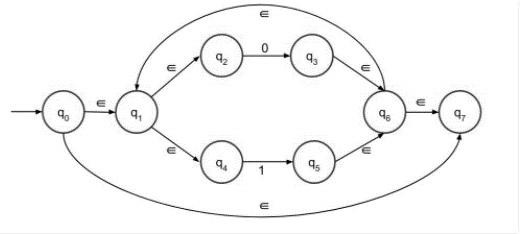
Second part − (00+11)
The second part can be easily drawn with the help of step 4.
In step 4, consider 1 and 0 both are either 00 or 11. Both strings are connected by + sign.
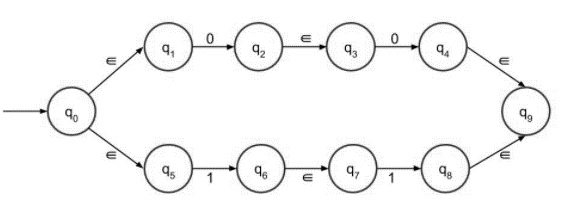
The final NFA with epsilon move is as follows −
Concatenate the first and second part,
12K+ Views
