Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct a Turing machine for adding 2 to the binary natural number?
A Turing machine (TM) can be formally described as seven tuples −
(Q,X, ∑, δ,q0,B,F)
Where,
Q is a finite set of states.
X is the tape alphabet.
∑ is the input alphabet.
δ is a transition function:δ:QxX->QxXx{left shift, right shift}.
q0 is the initial state.
B is the blank symbol.
F is the final state.
Input − n a natural number
Output − n + 2
Let’s represent natural numbers in unary form (e.g. 3 = 111, 5 = 11111) and 0 will be represented by the empty symbol.
Algorithm
Move the tape head to the left of the first 1 (if it exists).
Change that empty cell to a 1.
Move left and repeat.
Halt
We only need 3 states: 0 (initial), 1 and Halt; as well as three instructions −
(1): (0, 1, 1, L, 0) Move left to blank cell.
(2): (0, , 1, L, 1) Write 1 into the cell and move left.
(3): (1, ❑, 1, S, Halt) Write 1 into cell and halt.
Graphically, it is represented as follows:
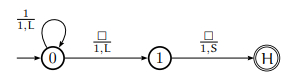
Instantaneous description
State 0: ❑ 1 1 1 ❑ Begin in state 0
State 0: ❑ 1 1 1 ❑ (1)
State 1: ❑ 1 1 1 1 ❑ (2)
Halt: ❑ 1 1 1 1 1 ❑ (3)
557 Views
