Design a push down automaton for L = {wwR | w ∈ {a, b}+}?

A pushdown automaton is used to implement a context-free grammar in the same way that we use a technique to design DFA for a regular grammar. A DFA work on a finite amount of information, where as a PDA works on an infinite amount of information.

Generally, a pushdown automaton is −

"Finite state machine" + "a stack"

A pushdown automaton consist of three components −

• an input tape,

• a control unit, and

• a stack with infinite size.

Now consider a problem that how to design push down automata for a given language −

Problem

Design a push down automaton which recognizes even length palindromes for L = {wwR | w ∈ {a, b}+}.

Solution

• Read in a string and save it to the stack.

• At each step, consider the possibility you might have reached the middle.

• Once reaching the midpoint, start working backwards, removing things from the stack if they match what was saved.

At each stop we need to test if we are in the middle of the string.

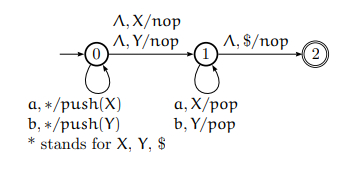
Step by step instantaneous descriptions for the string aabbaa are given below −

• Start → (0, aabbaa, $)

• Load stack → (0, abbaa, X$)

• Load stack → (0, bbaa, XX$)

• Load stack → (0, baa, YXX$)

• Try, is this the middle? → (1, baa, YXX$)

• Pop stack → (1, aa, XX$)

• Pop stack → (1, a, X$)

• Pop stack → (1, ∧, $)

• Done! → (2, ∧, $)