Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Design NPDA for accepting the language L = {am b(2m) | m>=1}
Basically a push down automata (PDA) is as follows −
“Finite state machine+ a stack”
PDA has three components, which are as follows −
- An Input tape.
- A control unit.
- A Stack with infinite size.
A PDA can be formally described as seven tuples
(Q, Σ,S, δ,q0,I,F)
Where,
- Q is finite number of states
- Σ is input alphabet
- S is stack symbol
- Δ is the transition function: QX(Σ∪{e})XSXQ
- q0 is the initial state (q0 belongs to Q)
- I is the initial state top symbol
- F is a set of accepting states (F belongs to Q)
Problem
Construct a non-deterministic PDA (NPDA) for accepting the language
L = {a^m b^{2m} | m>=1}.
Solution
The strings which are generated by this language are −
L = {abb, aabbbb, aaabbbbbb, aaaabbbbbbbb, ......}
The language counts the number of a’s followed by a double number of b’s.
Explanation
Step 1 − Maintain the order of a’s and b’s.
Step 2 − Construct a stack along with the state diagram.
Step 3 − The count of a’s and b’s is maintained by the stack.
Step 4 − The number of b’s is exactly double of the number of a’s.
Step 5 − We will take 2 stack alphabets:
r = { a, z }
Where,
- r = Set of all the stack alphabet
- z = Start symbol
Construction of PDA for the given problem
The PDA is as follows −
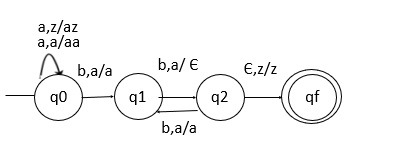
Transition functions
The transition functions for the PDA are as follows −
Design a NPDA, when ‘a’ comes before b then push it in stack and if again ‘a’ comes again push it. Also, when ‘b’ comes then pop one ‘a’ from the stack.
But we do this popping operation for alternate positions of b’s, (for two b’s we pop one ‘a’ and for four b’s we pop two ‘a’).
Finally, at the end if the stack becomes empty then we can say that the string is accepted by the PDA.
410 Views
