Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Average and RMS Value of Alternating Current and Voltage
Average Value of Alternating Quantity
The arithmetical average of all the instantaneous values of an alternating quantity over one cycle is known as the "Average Value of Alternating Quantity".
$$Average\:value=\frac{Sum\:of\:all\:instantaneous\:values\:over\:one\:cycle}{Number\:of\:instants}$$
$$=\frac{Total\:are\:under\:the\:curve\:for\:time\:period\:T}{Time\:Period\:(T)} $$
$$=\frac{i_{1}+i_{2}+i_{3}+...+i_{n}}{n}$$
Average Value of Symmetrical Waves
In case of symmetrical waves like sinusoidal voltage or current, the average value over one cycle is zero. It is because the positive half cycle is exactly equal to the negative half cycle. But the average value of positive or negative half cycle is not zero. Therefore, in case of symmetrical waves, the average value is calculated for half cycle.
$$Avg\:value = \frac{Sum\:of\:all\:instantaneous\:values\:over\:half\:cycle}{Number\:of\:instants\:of\:half\:cycle}$$
Average Value of Unsymmetrical Wave
In case of unsymmetrical waves like half wave rectified voltage, the average is calculated over the full cycle.
$$Avg\:value = \frac{Sum\:of\:all\:instantaneous\:values\:over\:half\:cycle}{Number\:of\:instants\:of\:one\:cycle}$$
Since the sinusoidal alternating voltages and currents are most wide used all over the world. Hence, we find the average and RMS values for the sinusoidal voltage and current.
Average Value of Sinusoidal Voltage or Current
The average value of AC (sinusoidal voltage or current) is the value of DC which would send the same amount of charge through the circuit for half cycle of the AC as is sent by the AC through the same circuit in the same time. It is denoted by Iav.
The average value of sinusoidal alternating voltage or current over one cycle is zero. It is because the area of positive half cycle is exactly equal to the area of negative half cycle. However, the average value over half cycle either positive or negative is not zero. Thus, the average value of sinusoidal voltage or current means half cycle average value.
Derivation – The average value of AC can be obtained by integrating the instantaneous values of current or voltage over the half cycle i.e. area of the curve over half cycle and dividing the result by base length of half cycle.
$$Average\:value=\frac{Area\:over\:half\:cycle}{base\:length\:of\:half\:cycle}$$
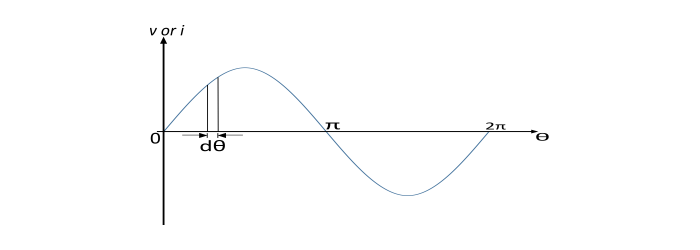
The equation of a sinusoidal varying voltage is given by
$$
u=V_{m}\sin\theta$$
Let us take a strip of thickness dθ in the positive half cycle of the wave. Consider v be the average height of the strip. Hence,
$$Area\:of\:Strip=
u\:d\theta$$
$$Area\:of\:half\:cycle=\int_{0}^{\pi}
u\:\sin\theta\:d\theta$$
$$=V_{m}[-\cos\theta]_0^\pi=2V_{m}$$
$$Average\:value(V_{a
u})=\frac{Area\:of\:half\:cycle}{Base\:length\:of\:half\:cycle}=\frac{2V_{m}}{\pi}=0.637V_{m}$$
Similarly, for Sinusoidal alternating current,
$$Average\:value(I_{a
u})=\frac{Area\:of\:half\:cycle}{Base\:length\:of\:half\:cycle}=\frac{2l_{m}}{\pi}=0.637l_{m}$$
Therefore, the average value of sinusoidal alternating current or voltage is equal to 0.637 times of the maximum or peak value.
RMS value of Sinusoidal Voltage or Current
The Root-Mean-Square (RMS) or Effective Value of a sinusoidal alternating current (AC) is the value of DC which when flowing through a given resistance for a given time produces the same amount of heat as produced by the AC when flowing through the same resistance for the same time.
RMS value = square 𝐫𝐨𝐨𝐭 of 𝐦𝐞𝐚𝐧 of the 𝐬𝐪𝐮𝐚𝐫𝐞𝐬 of the current
$$RMS\:value\:of\:alternating\:current\:(𝐼) =\sqrt{mean\:value\:of\:i^{2}}=\sqrt{\frac{i_{1}^{2}+i_{2}^{2}+i_{3}^{2}+...+i_{n}^{2}}{n}}$$
Similarly, RMS value of alternating voltage can be expressed as −
$$RMS\:value\:of\:alternating\:voltage\:(
u) =\sqrt{mean\:value\:of\:
u^{2}}=\sqrt{\frac{
u_{1}^{2}+
u_{2}^{2}+
u_{3}^{2}+...+
u_{n}^{2}}{n}}$$
For symmetrical waveforms, the RMS value can be calculated by considering halfcycle or full-cycle. But, in case of Unsymmetrical waveforms, full-cycle should be considered.
For symmetrical wave,
$$RMS\:value=\sqrt{\frac{Area\:of\:half\:cycle\:squared\:wave}{half\:cycle\:base\:length}}$$
RMS value of Sinusoidal Current or Voltage
Since the sinusoidal wave is a symmetrical wave. Hence we can calculate the RMS value of this by considering the half cycle only.
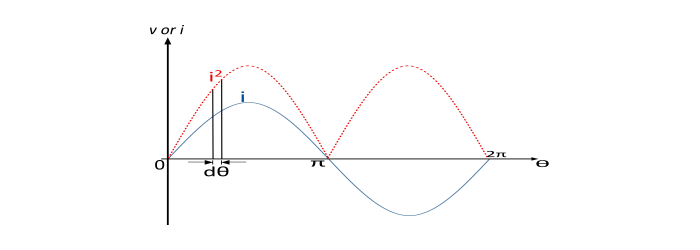
The equation of sinusoidal alternating current is given by
$$i=I_{m}\sin\theta$$
Let us consider a strip of width dθ in the positive half cycle of the squared current wave (shown red coloured dotted). Let the i2 be the average height of the strip.
$$Area\:of\:strip=i^{2}\:d\theta$$
$$Area\:of\:half\:cycle\:of\:squared\:wave=\int_{0}^{\pi}i^{2}\:d\theta=\int_{0}^{\pi}I_{m}^{2}\sin^{2}\theta\:d\theta$$
$$=I_{m}^{2}\int_{0}^{\pi}\sin^{2}\theta\:d\theta=\frac{\pi\:I^{2}m}{2}$$
Therefore,
$$I_{RMS}=\sqrt{\frac{Area\:of\:half\:cycle\:squared\:wave}{base\:length\:of\:half\:cycle}}=\sqrt{\frac{{\pi\:I_{m}^{2}}/{2}}{\pi}}=\frac{I_{m}}{\sqrt{2}}=0.707I_{m}$$
Similarly, the RMS value of sinusoidal alternating voltage is
$$V_{RMS}=\frac{V_{m}}{\sqrt{2}}=0.707V_{m}$$
Thus, the RMS value of sinusoidal alternating voltage or current is equal to 0.707 times of the peak value.
Numerical Example #1
A sinusoidal current has maximum value of 650 mA. What is its average value?
Solution
The average value of sinusoidal alternating current is given by
$$I_{a
u}=\frac{2I_{m}}{\pi}=0.637I_{m}$$
$$I_{a
u}=0.637 × 650 ×\:10^{-3}=414.05mA$$
Numerical Example #2
The equation of alternating voltage is given by ν = 325.22 𝑠𝑖𝑛314𝑡. Find (i) RMS value (ii) Frequency (iii) Average value.
Solution
The maximum value of the voltage is
$$V_{m}=325.22 V$$
RMS value of voltage
$$V_{RMS}=0.707𝑉𝑚 = 0.707 × 325.22 = 230 V$$
Frequency
$$\because\:\omega= 2𝜋𝑓 = 31$$
$$\therefore\:f=\frac{\omega}{2\pi}=\frac{314}{2\pi}=50 Hz$$
Average Value
$$V_{a
u}=0.637𝑉𝑚 = 0.637 × 325.22 = 207.2 V$$
26K+ Views
