Current Divider Rule and Voltage Divider Rule

Electric circuits are classified into two main types namely series circuit and parallel circuit based on the arrangement of components in the circuit. A series circuit is one in which the components are chain connected, while a parallel circuit is one in which all the circuit components are connected between two common points. Series circuits and parallel circuits act as voltage divider circuits and current divider circuits, respectively. Read through this article to find out more about Current Division Rule and Voltage Division Rule.

Current Division Rule

A parallel circuit acts as a current divider as it divides the total circuit current in its all branches. Figure1 shows a current divider circuit in which the total circuit current I has been divided into currents I₁ and I₂ in two parallel branches with resistances R₁ and R₂. Although, we can notice that the voltage drop across both resistances is same, i.e., V.

According to Ohm’s law,

$$\mathrm{I_{1}=\frac{V}{R_{1}}\: and\:I_{2}=\frac{V}{R_{2}} }$$

Let R is the equivalent resistance of the circuit, and it is given by,

$$\mathrm{R=\frac{R_{1}R_{2}}{R_{1}+R_{2}}\: \: \cdot\cdot\cdot\left ( 1 \right )}$$

Also, from the circuit, we get,

$$\mathrm{I=\frac{V}{R}=V\times \left ( \frac{R_{1}+R_{2}}{R_{1}R_{2}} \right )\: \:\cdot \cdot \cdot \left ( 2 \right )}$$

But, we know that the voltage across both resistances is same.

$$\mathrm{\therefore V=I_{1}R_{1}=I_{2}R_{2}\: \: \cdot \cdot \cdot \left ( 3 \right )}$$

Hence, from equations (2) & (3), we finally get,

$$\mathrm{ I=I_{1}R_{1}\left ( \frac{R_{1}+R_{2}}{R_{1}R_{2}} \right )=I_{1}\left ( \frac{R_{1}+R_{2}}{R_{2}} \right )}$$

$$\mathrm{\therefore I_{1}=\frac{IR_{2}}{R_{1}+R_{2}}\: \: \cdot \cdot \cdot \left ( 4 \right )}$$

Similarly,

$$\mathrm{ I=I_{2}R_{2}\left ( \frac{R_{1}+R_{2}}{R_{1}R_{2}} \right )=I_{2}\left ( \frac{R_{1}+R_{2}}{R_{1}} \right )}$$

$$\mathrm{\therefore I_{2}=\frac{IR_{1}}{R_{1}+R_{2}}\cdot \cdot \cdot \left ( 5 \right )}$$

Equations (4) and (5) give the expressions of current division rule. From these equations, we may state that the current in any of the parallel branches is equal to the ratio of opposite branch resistance to the sum of all resistances, multiplied by the total circuit current.

Voltage Division Rule

A series circuit acts as a voltage divider as it divides the total supply voltage into different voltages across the circuit elements. Figure2 shows a voltage divider circuit in which the total supply voltage V has been divided into voltages V₁ and V₂ across two resistances R₁ and R₂. Although, the current through both resistances is same, i.e., I.

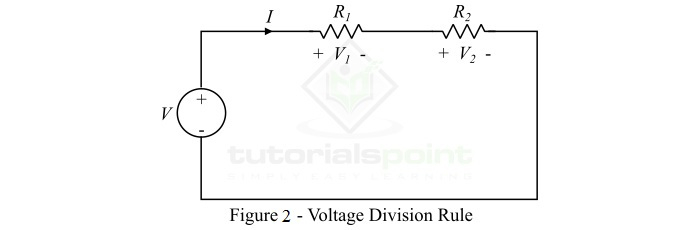
According to Ohm’s law,

$$\mathrm{V_{1}=IR_{1}\: and\: V_{2}=IR_{2}}$$

Let R is the total resistance of the circuit, and it is given by,

$$\mathrm{R=R_{1}+R_{2}\: \: \: \cdot\cdot \cdot \left ( 1 \right ) }$$

Also, from the circuit, we have,

$$\mathrm{V=IR=I\left ( R_{1}+R_{2} \right )\: \: \: \cdot\cdot \cdot \left ( 2 \right ) }$$

But

$$\mathrm{I=\frac{V_{1}}{R_{1}}=\frac{V_{2}}{R_{2}}\: \: \cdot \cdot \cdot \left ( 3 \right ) }$$

Therefore, from equations (2) & (3), we finally get,

$$\mathrm{V=\frac{V_{1}}{R_{1}}\left (R_{1}+R_{2}\right ) }$$

$$\mathrm{\therefore V_{1}=\frac{VR_{1}}{R_{1}+R_{2}}\: \: \cdot \cdot \cdot \left ( 4 \right )}$$

Similarly,

$$\mathrm{V=\frac{V_{2}}{R_{2}}\left (R_{1}+R_{2}\right ) }$$

$$\mathrm{\therefore V_{2}=\frac{VR_{2}}{R_{1}+R_{2}}\: \: \cdot \cdot \cdot \left ( 5 \right )}$$

Hence, from equations of voltage division rule, it may be said that the voltage across a resistor in a series circuit is equal to the product of the value of that resistor and the total supply voltage, divided by the total resistance of the series resistors.

Numerical Example (1)

Find the currents I₁ and I₂ in the parallel circuit shown in Figure3

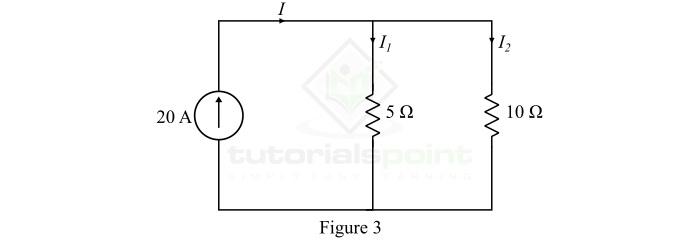
Solution

Using the current division rule, the current through resistor R₁ is,

$$\mathrm{I_{1}=I\times \frac{R_{2}}{R_{1}+R_{2}}=20\times \frac{10}{5+10}}$$

$$\mathrm{\therefore I_{1}=13.33\: A}$$

The current through resistor R₂ will be,

$$\mathrm{I_{2}=I\times \frac{R_{1}}{R_{1}+R_{2}}=20\times \frac{5}{5+10}}$$

$$\mathrm{\therefore I_{2}=6.67\: A}$$

Numerical Example (2)

Find the voltage across resistors R₁ and R₂ in the circuit shown in Figure-4.

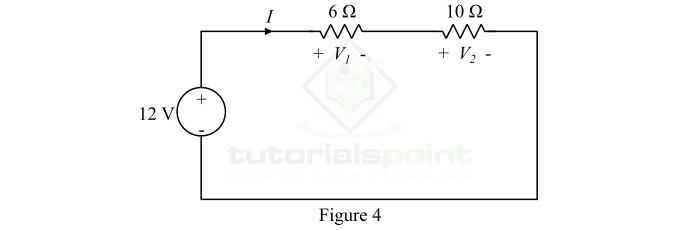
Solution

Using the voltage division rule, the voltage across resistor R₁ will be,

$$\mathrm{V_{1}=\frac{VR_{1}}{R_{1}+R_{2}}=\frac{12\times 6}{6+10}= 4.5 V}$$

The voltage across the resistor R₂ will be,

$$\mathrm{V_{2}=\frac{VR_{2}}{R_{1}+R_{2}}=\frac{12\times 10}{6+10}= 7.5 V}$$

Summary

The following points summarize what we discussed in this article −

• A parallel circuit acts as a current divider circuit because it divides the total circuit current in its all branches.

• A series circuit acts as a voltage divider circuit because it divides the total supply voltage in different voltages across various component of the circuit.

• The current division rule states that the current in any of the parallel branches of a parallel circuit is equal to the ratio of opposite branch resistance to the sum of all resistances, multiplied by the total current.

• The voltage division rule states that the voltage across any of the series components in a series circuit is equal to the product of value of that resistance and the total supply voltage, divided by the total resistance of the series circuit.