Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Overview of Electric Current, Voltage, and Resistance Electric Current
The directed flow of charge (free electrons) is called electric current. In other words, the electric current is defined as the rate of flow charge (free electrons). It is represented by 𝐼 or 𝑖 and measured in Amperes (A). i.e.
$$I=\frac{Q}{t}=\frac{ne}{t}\:\:Ampere(A)$$
Where, Q = ne, and e = 1.6 X 10-19 C.
In differential form,
$$i=\frac{dq}{dt}$$
How electric current flows?
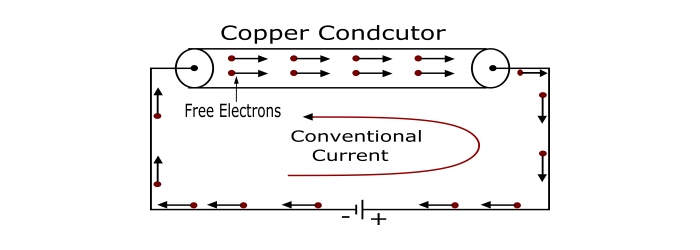
In the figure, the copper conductor has a large number of free electrons. When a potential difference (voltage) is applied across it, the free electrons (negatively charged) starts moving towards the positive terminal of the source. This directed flow free electrons is called as electric current.
The direction of actual current (or electron current) is from negative terminal to the positive terminal through the external circuit. But prior to the electron theory of matter, it was believed that the electric current was the flow of positive charge from positive terminal to the negative terminal via the external circuit. Therefore, this assumed direction of electric current is known as Conventional Current.
Types of Electric Current
The electric current can be classified in three types –
Steady Current
Varying Current
Alternating Current
Steady Current
An electric current whose magnitude does not change with time, it is called a steady current (Direct Current). The current provided by a cell or a battery is an example of steady current.
Varying Current
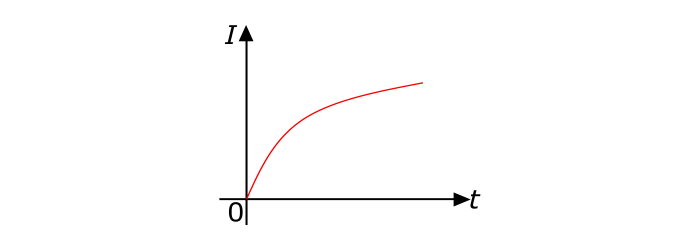
An electric current whose magnitude changes continuously with time, it is known as a Varying Current. The exponentially changing current (as in inductor) is an example of varying current.
Alternating Current
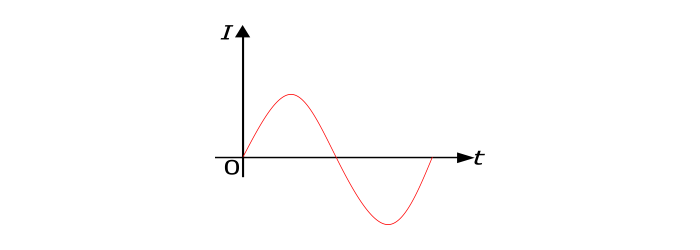
An electric current whose magnitude changes continuously with time and direction changes periodically, it is called as an Alternating Current. As this current flows in alternate directions in the circuit i.e. during half of time period in one direction and during the other half of time period in the opposite direction, for this reason it is called as alternating current.
Electric Potential
When a body is charged, work is done in charging it. This work done is stored in the body in the form of potential energy. Now, this charged body is able to move other charges by attraction or repulsion. Hence, it has ability to do work which is termed as electric potential of the body. i.e.
The ability of a charged body to do work is known as electric potential of the body. The measure of electric potential is given as the ratio of work done (W) to the charge (Q) i.e.
$$Electric \:Potential(V)=\frac{Work\:Done(W)}{Charge(Q}$$
The work done is measured in joules and charge in coulombs hence the unit of electric potential is joule/coulomb or Volt.
Potential Difference or Voltage
The difference in the potentials of the two charged bodies is known as potential difference.
The potential difference is also called Voltage. Hence, there is no such thing as a voltage at one point i.e. some reference must be used as the other point.
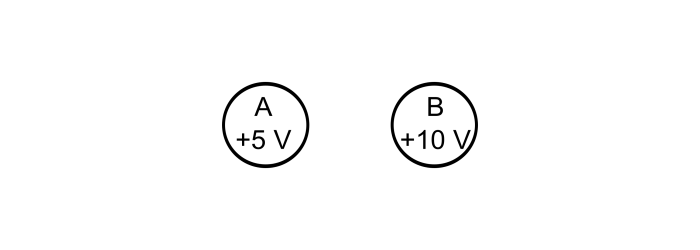
If two bodies have different electric potentials, a potential difference exists between them. Consider two bodies as shown in the above figure, the body A has potential of 5 V that means each coulomb of charge of body A has an energy of 5 joules while the body B has a potential of 10 V that means each coulomb of charge on the body B has an energy of 10 joules.
If the two bodies are joined through a wire, then electric current (conventional current) will flow from higher potential to lower potential i.e. from body B to body A. When the two bodies attain the same potential, the flow of current stops. Therefore, it can be said that, the electric current will flow in a circuit if potential difference exists. No voltage, no current flow.
Resistance
The measure of opposition offered by a substance to the flow of electric current (electrons) is called its Resistance. It is measured in Ohms (Ω). The circuit symbol of resistance is shown in the figure below.
As the electric current is flow of electrons, hence the resistance is the opposition offered by substance to the flow of these electrons. Since the resistance is the electric friction offered by the substance and causes production of heat with flow of electric current.
Factors affecting the resistance
The resistance of a conductor is directly proportional to its length (𝑙).
The resistance if a conductor is inversely proportional to its cross-sectional area (a).
The resistance depends upon the nature of material of the conductor.
The resistance changes with the change in temperature.
Hence, from the first three points, we get,
$$R\propto\frac{l}{a}$$
$$R=\rho\frac{l}{a}$$
Where, ρ(Rho) = is a constant and is known as Resistivity or Specific Resistance. Its value depends upon the nature of the material. The unit of ρ is Ohm-meter (Ω-m).
Effect of Temperature on Resistance
On Pure Metals (Conductors) – The resistance of pure metals like copper, aluminium etc. increases with the increase of temperature. The temperature/resistance curve for pure metals is straight line. As the resistance of pure metals increases with the increase of temperature, hence they have positive temperature co-efficient of resistance.
On Insulators, Semi-Conductors and Electrolytes – The resistance of these materials decreases with the increase of the temperature. Therefore, these materials have negative temperature co-efficient of resistance.
On the Alloys – The resistance of alloys increases with the rise in temperature but this increase is small and irregular, that is practically negligible over a wide range of temperatures.
Numerical Example #1
Find the current in a conductor when 2.56 X 1017 electrons pass through it in 65 ms.
Solution
$$Current(I)=\frac{Q}{t}=\frac{ne}{t}=\frac{(2.56\times\:10^{17})\times\:(1.6\times\:10^{-19})}{65\times\:10^{-3}}$$
$$=630\times\:10^{-3}A=630mA$$
Numerical Example #2
The potential difference across a battery is 12 V. How much charge it deliver to do 60 J of work.
Solution
$$Charged \:delivered(Q)=\frac{W}{V}=\frac{60}{12}=5C$$
Numerical Example #3
Calculate the resistance of 500 meters length of a wire having a uniform cross sectional area of 0.69 cm2 . The wire is made of copper having resistivity of 1.7 × 10-6Ω − cm.
Solution
$$R=\rho\frac{l}{a}=(1.7\times\:10^{-6})\times\:\frac{500}{0.69\times\:10^{-4}}=12.32\Omega$$
498 Views
