
- Digital Signal Processing Tutorial
- DSP - Home
- DSP - Signals-Definition
- DSP - Basic CT Signals
- DSP - Basic DT Signals
- DSP - Classification of CT Signals
- DSP - Classification of DT Signals
- DSP - Miscellaneous Signals
- Operations on Signals
- Operations Signals - Shifting
- Operations Signals - Scaling
- Operations Signals - Reversal
- Operations Signals - Differentiation
- Operations Signals - Integration
- Operations Signals - Convolution
- Basic System Properties
- DSP - Static Systems
- DSP - Dynamic Systems
- DSP - Causal Systems
- DSP - Non-Causal Systems
- DSP - Anti-Causal Systems
- DSP - Linear Systems
- DSP - Non-Linear Systems
- DSP - Time-Invariant Systems
- DSP - Time-Variant Systems
- DSP - Stable Systems
- DSP - Unstable Systems
- DSP - Solved Examples
- Z-Transform
- Z-Transform - Introduction
- Z-Transform - Properties
- Z-Transform - Existence
- Z-Transform - Inverse
- Z-Transform - Solved Examples
- Discrete Fourier Transform
- DFT - Introduction
- DFT - Time Frequency Transform
- DTF - Circular Convolution
- DFT - Linear Filtering
- DFT - Sectional Convolution
- DFT - Discrete Cosine Transform
- DFT - Solved Examples
- Fast Fourier Transform
- DSP - Fast Fourier Transform
- DSP - In-Place Computation
- DSP - Computer Aided Design
- Digital Signal Processing Resources
- DSP - Quick Guide
- DSP - Useful Resources
- DSP - Discussion
DSP - Operations on Signals Integration
Integration of any signal means the summation of that signal under particular time domain to get a modified signal. Mathematically, this can be represented as −
$$x(t)\rightarrow y(t) = \int_{-\infty}^{t}x(t)dt$$Here also, in most of the cases we can do mathematical integration and find the resulted signal but direct integration in quick succession is possible for signals which are depicted in rectangular format graphically. Like differentiation, here also, we will refer a table to get the result quickly.
| Original Signal | Integrated Signal |
|---|---|
| 1 | impulse |
| Impulse | step |
| Step | Ramp |
Example
Let us consider a signal $x(t) = u(t)-u(t-3)$. It is shown in Fig-1 below. Clearly, we can see that it is a step signal. Now we will integrate it. Referring to the table, we know that integration of step signal yields ramp signal.
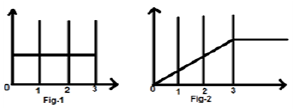
However, we will calculate it mathematically,
$y(t) = \int_{-\infty}^{t}x(t)dt$
$= \int_{-\infty}^{t}[u(t)-u(t-3)]dt$
$= \int_{-\infty}^{t}u(t)dt-\int_{-\infty}^{t}u(t-3)dt$
$= r(t)-r(t-3)$
The same is plotted as shown in fig-2,