- Data Mining Tutorial
- Data Mining - Home
- Data Mining - Overview
- Data Mining - Tasks
- Data Mining - Issues
- Data Mining - Evaluation
- Data Mining - Terminologies
- Data Mining - Knowledge Discovery
- Data Mining - Systems
- Data Mining - Query Language
- Classification & Prediction
- Data Mining - Decision Tree Induction
- Data Mining - Bayesian Classification
- Rules Based Classification
- Data Mining - Classification Methods
- Data Mining - Cluster Analysis
- Data Mining - Mining Text Data
- Data Mining - Mining WWW
- Data Mining - Applications & Trends
- Data Mining - Themes
- DM Useful Resources
- Data Mining - Quick Guide
- Data Mining - Useful Resources
- Data Mining - Discussion
Miscellaneous Classification Methods
Here we will discuss other classification methods such as Genetic Algorithms, Rough Set Approach, and Fuzzy Set Approach.
Genetic Algorithms
The idea of genetic algorithm is derived from natural evolution. In genetic algorithm, first of all, the initial population is created. This initial population consists of randomly generated rules. We can represent each rule by a string of bits.
For example, in a given training set, the samples are described by two Boolean attributes such as A1 and A2. And this given training set contains two classes such as C1 and C2.
We can encode the rule IF A1 AND NOT A2 THEN C2 into a bit string 100. In this bit representation, the two leftmost bits represent the attribute A1 and A2, respectively.
Likewise, the rule IF NOT A1 AND NOT A2 THEN C1 can be encoded as 001.
Note − If the attribute has K values where K>2, then we can use the K bits to encode the attribute values. The classes are also encoded in the same manner.
Points to remember −
Based on the notion of the survival of the fittest, a new population is formed that consists of the fittest rules in the current population and offspring values of these rules as well.
The fitness of a rule is assessed by its classification accuracy on a set of training samples.
The genetic operators such as crossover and mutation are applied to create offspring.
In crossover, the substring from pair of rules are swapped to form a new pair of rules.
In mutation, randomly selected bits in a rule's string are inverted.
Rough Set Approach
We can use the rough set approach to discover structural relationship within imprecise and noisy data.
Note − This approach can only be applied on discrete-valued attributes. Therefore, continuous-valued attributes must be discretized before its use.
The Rough Set Theory is based on the establishment of equivalence classes within the given training data. The tuples that forms the equivalence class are indiscernible. It means the samples are identical with respect to the attributes describing the data.
There are some classes in the given real world data, which cannot be distinguished in terms of available attributes. We can use the rough sets to roughly define such classes.
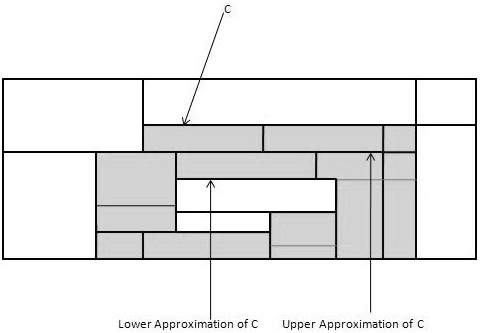
For a given class C, the rough set definition is approximated by two sets as follows −
Lower Approximation of C − The lower approximation of C consists of all the data tuples, that based on the knowledge of the attribute, are certain to belong to class C.
Upper Approximation of C − The upper approximation of C consists of all the tuples, that based on the knowledge of attributes, cannot be described as not belonging to C.
The following diagram shows the Upper and Lower Approximation of class C −
Fuzzy Set Approaches
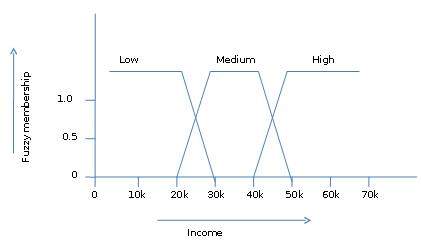
Fuzzy Set Theory is also called Possibility Theory. This theory was proposed by Lotfi Zadeh in 1965 as an alternative the two-value logic and probability theory. This theory allows us to work at a high level of abstraction. It also provides us the means for dealing with imprecise measurement of data.
The fuzzy set theory also allows us to deal with vague or inexact facts. For example, being a member of a set of high incomes is in exact (e.g. if $50,000 is high then what about $49,000 and $48,000). Unlike the traditional CRISP set where the element either belong to S or its complement but in fuzzy set theory the element can belong to more than one fuzzy set.
For example, the income value $49,000 belongs to both the medium and high fuzzy sets but to differing degrees. Fuzzy set notation for this income value is as follows −
mmedium_income($49k)=0.15 and mhigh_income($49k)=0.96
where ‘m’ is the membership function that operates on the fuzzy sets of medium_income and high_income respectively. This notation can be shown diagrammatically as follows −