Data Mining - Decision Tree Induction

A decision tree is a structure that includes a root node, branches, and leaf nodes. Each internal node denotes a test on an attribute, each branch denotes the outcome of a test, and each leaf node holds a class label. The topmost node in the tree is the root node.

The following decision tree is for the concept buy_computer that indicates whether a customer at a company is likely to buy a computer or not. Each internal node represents a test on an attribute. Each leaf node represents a class.

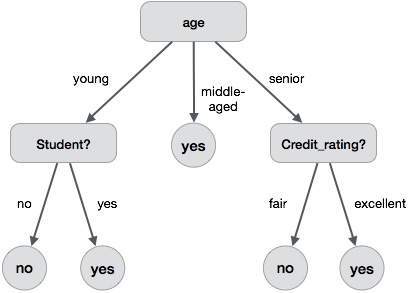
Decision Tree

The benefits of having a decision tree are as follows −

  • It does not require any domain knowledge.
  • It is easy to comprehend.
  • The learning and classification steps of a decision tree are simple and fast.

Decision Tree Induction Algorithm

A machine researcher named J. Ross Quinlan in 1980 developed a decision tree algorithm known as ID3 (Iterative Dichotomiser). Later, he presented C4.5, which was the successor of ID3. ID3 and C4.5 adopt a greedy approach. In this algorithm, there is no backtracking; the trees are constructed in a top-down recursive divide-and-conquer manner.

Generating a decision tree form training tuples of data partition D
Algorithm : Generate_decision_tree

Input:
Data partition, D, which is a set of training tuples 
and their associated class labels.
attribute_list, the set of candidate attributes.
Attribute selection method, a procedure to determine the
splitting criterion that best partitions that the data 
tuples into individual classes. This criterion includes a 
splitting_attribute and either a splitting point or splitting subset.

Output:
 A Decision Tree

Method
create a node N;

if tuples in D are all of the same class, C then
   return N as leaf node labeled with class C;
   
if attribute_list is empty then
   return N as leaf node with labeled 
   with majority class in D;|| majority voting
   
apply attribute_selection_method(D, attribute_list) 
to find the best splitting_criterion;
label node N with splitting_criterion;

if splitting_attribute is discrete-valued and
   multiway splits allowed then  // no restricted to binary trees

attribute_list = splitting attribute; // remove splitting attribute
for each outcome j of splitting criterion

   // partition the tuples and grow subtrees for each partition
   let Dj be the set of data tuples in D satisfying outcome j; // a partition
   
   if Dj is empty then
      attach a leaf labeled with the majority 
      class in D to node N;
   else 
      attach the node returned by Generate 
      decision tree(Dj, attribute list) to node N;
   end for
return N;

Tree Pruning

Tree pruning is performed in order to remove anomalies in the training data due to noise or outliers. The pruned trees are smaller and less complex.

Tree Pruning Approaches

There are two approaches to prune a tree −

  • Pre-pruning − The tree is pruned by halting its construction early.

  • Post-pruning - This approach removes a sub-tree from a fully grown tree.

Cost Complexity

The cost complexity is measured by the following two parameters −

  • Number of leaves in the tree, and
  • Error rate of the tree.
Advertisements